Dolmetsch Online - Physics of Musical Instruments


physics of musical instruments	a brief history
Dr. Brian Blood

home :: resources :: music theory & history :: recorder lessons :: music dictionary :: physics of musical instruments :: e-monographs	what you think of our site?

topics on this page :: how we arrive at our present day understanding of sound	site map :: quick search

If I have seen further than other men, it is because I have stood on the shoulders of giants
Isaac Newton (1642-1727) English mathematician and physicist

Pythagoras
born: about 569 BC in Samos, Ionia
died: about 475 BC in Metapontum, Italy

Aristotle
born: 384 BC in Stagirus, Macedonia, Greece
died: 322 BC in Chalcis, Euboea, Greece

Anicius Manlius Severinus Boethius
born: 480 in or near Rome, Italy
died: 524 or 525 in Pavia, Italy

Recommended Links
Boethius
Boethius Links

Sir Francis Bacon
born: 22 Jan 1561 in London
died: 9 April 1626 in Highgate, nr. London

Galileo Galilei
born: 15 Feb 1564 in Pisa
died: 8 Jan 1642 in Arcetri (nr. Florence)

Christiaan Huygens
born: 14 April 1629 in The Hague, Netherlands
died: 8 July 1695 in The Hague, Netherlands

Recommended Links
Christiaan Huygens
Christiaan Huygens

Marin Mersenne
born: 8 Sept 1588 in Oize in Maine, France
died: 1 Sept 1648 in Paris, France

Samuel Pepys
born: 23 Feb 1633 in London
died: 26 May 1703 in Clapham

Recommended Links
Samuel Pepys
Pepys' Diary

Democritus of Abdera
born: 460 BC in Abdera, Thrace, Greece
died: c. 370 BC

Recommended Links
Democritus of Abdera

Pierre Gassendi
born: 22 Jan 1592 in Champtercier, France
died: 24 Oct 1655 in Paris, France

Recommended Links
Lord Rayleigh

"The history of science like the history of all human ideas is a history of irresponsible dreams, of obstinacy, of error. But science is one of the very few human activities - perhaps the only one - in which errors are systematically criticized and fairly often in time corrected. (Karl Popper)

When examining the scientific ideas of earlier times, we must be careful not to project our own present ideas and understanding onto the past. If we are to distinguish between the scientific knowledge we possess today and that in times past, we must understand what a 'reasonable' man living many hundreds of years ago could 'demonstrate that he knew', on the basis of those experiences he was likely to have had, and on his knowledge and understanding of those authorities who came before him. We must also appreciate the questions he might ask and the thoughts he might have for "discovery consists of seeing what everybody has seen but thinking what nobody has thought."

We should be aware too of the nature of medieval university education, based on the seven liberal arts (septem artes liberales), as originally set out by St. Jerome (340/2-420), Martianus Capella (fl. fifth century), and St. Augustine of Hippo (354-430), and described in the sixth century by Cassiodorus.

He [Cassiodorus] distinguishes the arts, notably grammar and rhetoric, from the sciences, which are arithmetic, geometry, music, and astronomy. Dialectics, to which he attributes great importance, he considers part art and part science

The liberal arts were organised in the following way:

The Trivium: Grammar, Rhetoric, Dialectic;
The Quadrivium: Music, Arithmetic, Geometry, Astronomy.

A student might study the Trivium for four years and the Quadrivium for three and the importance of mathematics in all this is clear.

"He who knows not mathematics cannot know the other sciences nor the things of this world ... And, what is worse, those who have no knowledge of mathematics do not perceive their own ignorance and so do not look for a cure. Conversely a knowledge of this science prepares the mind and raises it up to a well-authenticated knowledge of all things. " (Roger Bacon)

We need to differentiate philosophy, a system of knowledge regulated by reason, theology, a body of revealed truth held of faith, and metaphysics which tended to confuse the two but which Aristotle (384-322 B.C.) called 'a science of what is simply in its character of Being and the properties which it has as such'.

New 'experiences' could lead to 'new science' and to 'new philosophy', but many of the intellectual achievements of earlier times might be retained, sometimes unchanged, sometimes remoulded or reinterpreted to suit more modern times. Many studying the history of science take this point for granted but it is only rarely articulated. However, it is vital to any fair treatment of the past, a past we can view only from where we stand now, that we appreciate that, to paraphrase Soren Kierkegaard (1813-1855), 'the irony of life is that it is lived forwards but understood backwards'.

Ref: Medieval Thought by Gordon Leff, Penguin Books [1958]
Ref: Structure of Scientific Revolutions by Thomas Kuhn, University of Chicago Press [1970]
Ref: The Beginnings of Western Science by David C. Lindberg, University of Chicago Press [1992]
Ref: Sixty Methodological Potholes

The Greeks developed theories to explain almost every aspect of human experience. In his essay entitled The Classification of the Arts, W. Tatarkiewicz observes:

The Greeks included music together with poetry in the sphere of inspiration. First, there was a psychological affinity between the two arts; both were comprehended as acoustic productions, and both were supposed to have a manic character, i.e., to be the source of rapture. Second, they were practised jointly since poetry was sung and music was vocalised, and since both were essential elements of mysteries". Before the ancient idea of art became modern, two things were to happen: poetry and music were to be incorporated into art, while handicrafts and sciences were to be eliminated from it. The first happened before the end of antiquity. Poetry and music could indeed be considered arts as soon as their rules were discovered. This happened early so far as music is concerned: since the Pythagoreans found the mathematical laws of acoustic harmony, music has been considered as a branch of knowledge as well as an art.

For many centuries we have accepted that Pythagoras was a seminal figure in the field of Greek music theory, much of it strongly metaphysical. The association of Pythagoras with the many ideas in this field ascribed to him has been examined and questioned by Walter Burkert in his monumental study Weisheit und Wissenschaft: Studien zu Pythagoras, Philolaus und Platon. However, there is little doubt that his school subscribed to a series of philosophical beliefs including that at its deepest level, reality is mathematical in nature

Pythagoreans believed that harmony was divine ("harmony of the spheres" was a Pythagorean metaphor for the association between man, music, mathematics and the universe, although there is no evidence that Pythagoras himself used an expression which is known only from writings set down many decades after Pythagoras' death) and, that through its cathartic effect, music was a medicine that could cure ills. Their dream of reducing the formulation of the laws of nature to a consideration of pure numbers and simple ratios persisted even into the seventeenth century as the extract from Peter Sterry's A Discourse of the Freedome of the Will (1675) demonstrates:

Being it self, in its universal Nature, from its purest heighth, by beautiful, harmonious, just degrees and steps, descendeth into every Being, even to the lowest shades. All ranks and degrees of Being, so become like the mystical steps in that scale of Divine Harmony and Proportions, Jacobs Ladder. Every form of Being to the lowest step, seen and understood according to its order and proportions in its descent upon this Ladder, seemeth as an Angel, or as a Troop of Angels in one, full of all Angelick Musick and Beauty.

Ref: Catharsis
Ref: The Classification of the Arts

The Greeks investigated the harmonic relationships between vibrating strings of different lengths using the monochord.

The monochord, said to have been invented by Pythagoras and illustrated above, was a rectangular box-shaped instrument, with two fixed bridges (shown in black) across which a single string passed. One end of the string was wound around a peg while the other end was looped over a small metal pin driven into the frame of the box. The string's tautness was adjusted by turning the peg. The string could be bowed or plucked and a moveable bridge (shown in red), lying between the two fixed bridges, divided the string into two shorter lengths. When the moveable bridge was placed exactly half way between the fixed bridges, the two shorter lengths would sound the same note; the ratio of the two 'half-lengths' was then 1:1. If the moveable bridge was placed one third of the distance between the fixed bridges, so that the string was divided in the ratio 2:1, the two strings would now sounded one octave apart, the longer string sounding the lower note. In this way it was found that the ratio 2:3 (called 'hemiolic', which means the whole exceeded by its half) was associated with the interval of a fifth and 3:4 (called 'epitrite', which means the whole exceeded by its third) gave an interval of a fourth.

The discovery that musical harmonies are themselves numerical ratios, that the 'consonant' harmonies are represented by ratios of the four integers 1, 2, 3 and 4 (for which Pythagoras had a particular regard), and that a string or flute shortened to half of its original length produces a note which is one octave higher was seen as confirming their metaphysical idea that number is the actual essence of things.

Aristotle, tutor to the young Alexander the Great, explained the production and transmission of sound in terms of motion, "thrusting forward in like manner the adjoining air, to that the sound travels unaltered in quality as far as the disturbance of the air manages to reach", whether the motion of the object that generated the sound, or the motion of the medium through which that sound might travel, or the motion of receptors within the body, in particular within the ear, to explain the process we call 'hearing'. Modern physics, in the main, owes little to the scientific concepts of the ancient Greeks, but the physics of sound has retained a strong sense of many of their ideas including the proposition that sound is a 'mechanical wave' analogous in some way to a wave traveling over water, although the insights we have today into what sound is, how it travels and the physiological and psychological subtleties of the 'auditory process', are more profound than any ancient Greek could have imagined.

Ref: Music Theory Online - Chapter 25 - Notes & Harmonies
Ref: Weisheit und Wissenschaft: Studien zu Pythagoras, Philolaus und Platon (1962) - Walter Burkert
Ref: Music Theory Online - Chapter 27 - Pitch, Temperament & Timbre

Medieval thought was dominated by the works of Aristotle, not so much in the original Greek but through subsequent Latin and Arabic commentaries, especially those of St. Augustine (354-430), Flavius Magnus Aurelius Cassiodorus Senator (c.490-c.583) - whose exposition on the theory of music in antiquity, Institutiones musicæ, borrowed from the works, now lost, of Roman author Albinus - Anicius Manlius Severinus Boethius (480-524 or 525), St. Thomas Aquinas (1226-1274) and the great Jewish and Arabic thinkers of the tenth, eleventh and twelfth centuries including Al-Farabi (872-950), Avicenna (980-1037), Averroes (1126-1178), Avicebrol (c.1020-1070) and Maimonides (1135-1204). Even those commentaries were new editions prepared in the sixteenth century by printers like Wolff of Basle, who, between 1501 and 1515, produced five massive volumes of the Summae of medieval Doctors.

Ref: The Emergence of Scientific Literature and Quantification 1520-1560 by Dr. Kim H. Veltman

A recurrent concern of philosophers was the proper boundary between faith and reason, between areas of human experience that were matters of revelation and should be accepted as 'the way things are' and those matters that might be questioned and subjected to 'the searchings of the reasoning mind' - see, for example, The Doctrine of Double Truth. Tertullian (Quintus Septimus Florens Tertullianus, second and third century), a theologian of the early Catholic church, tells us that 'we have no need for curiosity, after Jesus Christ, nor of investigation after the Gospel'. Modern science in Europe emerged, however, in mid-thirteenth century Paris, when an Oxford-educated Franciscan, Roger Bacon (c. 1220-1292), posited that questions about nature could be answered by observation and not only by recourse to the Bible. Almost certainly, Bacon's was influenced by the writings of the great Muslim scientist Alhazan (Abu Ali al-Hasan ibn al-Hasan ibn al-Haytham) (c.9651038) who may have been the first person to test hypotheses with verifiable experiments, thereby developing the scientific method more than 200 years before European scholars learned of it by reading his books.

Alhazan's study of light and vision, Kitâb al-Manâzir (Book of Optics) was translated into Latin as De aspectibus in late thirteenth century Spain. Copies of the book circulated throughout Europe. Roger Bacon wrote a summary of it entitled Perspectiva (Optics).

It has been pointed out that, for medieval scholars, the writings of the ancients carried the 'authority of history', that in some way their very survival was testament to their veracity. Dante Alighieri (1265-1321) praised Aristotle as 'the Master of those that know' but the Greek philosopher's opinions in many areas of science were to prove, in the main, defective and a hindrance to the new science of the seventeenth century. This stumbling block was all the more troublesome because the dominant intellectual force in medieval and Renaissance Europe, authoritarian conservative Catholicism, was caste in a Thomist-Aristotelian mould and would not lightly give up these certainties, seen as matters of faith - nor admit to error.

Steven Kreis, in his article Renaissance Humanism writes:

" ... the man of the Renaissance lived, as it were, between two worlds. The world of the medieval Christian matrix, in which the significance of every phenomenon was ultimately determined through uniform points of view, no longer existed for him. On the other hand, he had not yet found in a system of scientific concepts and social principles stability and security for his life. In other words, Renaissance man may indeed have found himself suspended between faith and reason.

As the grip of medieval supernaturalism began to diminish, secular and human interests became more prominent. The facts of individual experience in the here and now became more interesting than the shadowy afterlife. Reliance upon faith and God weakened. Fortuna (chance) gradually replaced Providence as the universal frame of reference. The present world became an end in itself instead of simply preparation of a world to come. Indeed, as the age of Renaissance humanism wore on, the distinction between this world (the City of Man) and the next (the City of God) tended to disappear.

However, by the end of the seventeenth century, in his Dictionnaire Historique et Critique, Pierre Bayle (1647-1706) was insisting that the antiquity of a belief was no guarantee of its veracity.

Ref: Double Truth - the doctrine of Double Truth first appeared in 1277
Ref: Ancients and Moderns in the Eighteenth Century
Ref: Pierre Bayle - E-Texts

Subscribing to Pierre Bayles dictum, the great multi-volumed illustrated Encyclopèdie, ou Dictionnaire raisonné des sciences, des arts et des métiers, par une société de gens de lettres, edited by Jean le Rond d'Alembert (1717-1783) and Denis Diderot (1713-1784), which appeared in Paris between 1751 and 1780, and to which the philosophes Voltaire (1694-1778), Baron de Montesquieu (1689-1755), Anne Robert Jacques Turgot (1727-1781), Jean-Jacques Rousseau (1712-1778) and others contributed, includes, in its Preliminary Discourse, an 'eighteenth-century view' of the history of the sciences and the arts.

Sir Francis Bacon (1561-1626), Lord Chancellor to King James I of England, is seen as the 'father' of the scientific method. d'Alembert writes of Bacon's The Advancement of Learning: "(In it)... he perfects the views that he had presented in his first book, carries them further, and makes known the necessity of experimental physics, of which no one was yet aware". For Bacon, this was the Novum Organum, the 'new tool'.

Ref: Preliminary Discourse to the Encyclopedia by d'Alembert, translated by R.N. Schwab, pub. Bobbs-Merrill [1963]

Sir Francis Bacon gives us an illuminating portrait of himself in the Preface to De Interpretatione Naturae (1620).

"Now if a man should succeed, not in striking out some new invention, but in kindling a light in nature - a light that should eventually disclose and bring into sight all that is most hidden and secret in the universe - that man (I thought) would be benefactor indeed of the human race ... For myself I found that I was fitted for nothing so well as the study of truth, as having a mind nimble and versatile enough to catch the resemblances of things (which is the chief point) and at the same time steady enough to fix and distinguish their subtler differences; as being gifted by nature with desire to seek, patience to doubt, fondness to meditate, slowness to assert, readiness to reconsider, carefulness to dispose and set in order; and as being a man that neither affects what is new nor admires what is old, and hates every kind of imposture. So I thought that my mind had a kind of familiarity and relationship with truth"

We have moved significantly from 'passive observation', Roger Bacon's proposal, to 'experimentation', the new 'scientific method' where 'if a man will begin with certainties, he will end in doubts; but if he will be content to begin with doubts, he will end in certainties.'

In late sixteenth and early seventeenth century Italy, Vincenzo and Galileo Galilei were to apply this 'modus operandum' to devastating effect. Vincenzo belonged to a noble family of straitened fortune, and had gained some distinction as a musician and mathematician. In Dialogo della musica antica et della moderna, published in Venice in 1581, Vincenzo set out the philosophy which had directed his life.

"It appears to me that they who in proof of any assertion rely simply on the weight of authority, without adducing any argument in support of it, act very absurdly. I, on the contrary, wish to be allowed freely to question and freely to answer without any sort of adulation, as well as becomes those who are sincere in the search of truth."

The character of Vincenzo was of someone prepared to challenge those who relied on 'received wisdom' and turned their backs on observation and experiment, ignoring the philosophy expounded by the ancient sage Protagoras (c.490-c.420BC), that 'perception is truth', and that 'man is the measure of all things', the origin of 'relativism'. Vincenzo's contemporary Zarlino, defended the old, established Aristotelian philosophy, set out in the De institutione musica of Anicius Manlius Severinus Boethius, which influenced greatly musical theory and aesthetics throughout the Medieval period.

Vincenzo was drawn to the ideas of Aristoxenus (364-304BC), one of Aristotle's most brilliant pupils, who rejected the Pythagorean-Platonic tradition including the necessary representation of intervals by numerical ratios, and chose instead to consider harmony as it is perceived by the ear.

"[on the subject of temperaments] such contortions are nonsense, Galilei countered. All scales are man-made, with no basis in nature whatsoever. Indeed, just intonation is itself only an ideal; in practice singers automatically temper their intervals for the sake of overall harmony. Zarlino responded by calling Galilei's treatise "an assault on God's plan."

Reference:

Ruth Franklin, a review of: "Temperament: The Idea That Solved Music's Greatest Riddle" (2001)

Many of Vincenzo's opinions were refined through his correspondence with Girolamo Mei who summed up the emancipation of music from scientific determinism in a letter to Vincenzo Galilei dated 1572:

The true end of science is altogether different from that of art.... The science of music goes about diligently investigating and considering all the qualities and properties of the existing constitution and ordering of musical tones, whether these are simple qualities or comparative, like the consonances, and this for no other aim than to come to know the truth itself, the perfect goal of all speculation, and as a by-product the false. It then lets art exploit as it sees fit, without any limitation, those tones about which science has learned the truth.

Vincenzo had seven children. Galileo was the oldest of three sons. Bearing in mind that Galileo's later years were overshadowed by his dispute with the Inquisition (the body set up by the Catholic Church to enforce intellectual and religious conformity), it is instructive to read the following extract from Galileo's biography in the Catholic Encyclopedia.

"It is the great merit of Galileo that, happily combining experiment with calculation, he opposed the prevailing system according to which, instead of going directly to nature for investigation of her laws and processes, it was held that these were best learned by authority, especially by that of Aristotle, who was supposed to have spoken the last word upon all such matters, and upon whom many erroneous conclusions had been fathered in the course of time.

Against such a superstition Galileo resolutely and vehemently set himself, with the result that he not only soon discredited many beliefs which had hitherto been accepted as indisputable, but aroused a storm of opposition and indignation amongst those whose opinions he discredited; the more so, as he was a fierce controversialist, who, not content with refuting adversaries, was bent upon confounding them. Moreover, he wielded an exceedingly able pen, and unsparingly ridiculed and exasperated his opponents. Undoubtedly he thus did much to bring upon himself the troubles for which he is now chiefly remembered.

As Sir David Brewster (Martyrs of Science) says, "The boldness, may we not say the recklessness, with which Galileo insisted on making proselytes of his enemies, served but to alienate them from the truth".

Like his father Vincenzo and younger brother Michelangelo, Galileo was a fine lutenist and also played the organ. In later life, he used to say that had he been free to choose his profession, he would have become a painter. He retained a love of poetry but was a severe critic of those poets whose work he did not like. He wrote that reading Tasso after Ariosto was like eating 'cucumbers after melons'. Malatesti's volume of poetry, Sphinx, is prefaced by Galileo's sonnet on the telescope. It was this volume that Malatesti gifted to the poet John Milton when the Englishman was on a trip to Italy.

A few years before losing his sight, Galileo had the manuscript of Discourses Concerning Two New Sciences, dedicated to Count de Noailles, the French Ambassador in Rome, smuggled out of Italy and delivered to the printer Elzevir of Leiden in Holland. The book, which finally appeared in 1638, set out his new science of motion (including his ideas on the vibration of bodies), his studies on the strength of materials and the physics of the pendulum.

Galileo's last pupil and first biographer, Vincenzo Viviani, tells us that his study of pendulums began after watching a suspended lamp swinging back and forth in the cathedral of Pisa, in 1581, where as a student of barely a few months standing, he was studying at the University for a degree in medicine. It was the periodicity and the isochronicity of the motion that struck his attention (the period being the time taken to return to the position from which it had been released). He checked the period of swing against his own pulse and saw that it remained unchanged no matter how 'wide' the swing (this property is what we term 'isochronicity). He experimented at home using a weight on the end of a length of string. By shortening the string, he discovered the relationship between the string's length and period of the 'swing'.

In all probability Galileo was not the first to be aware of the ability of pendulums to 'keep time'. Leonardo da Vinci had guessed this almost a hundred years earlier. Galileo was, however, the first to see how a system exhibiting a natural 'period' or 'frequency' ('frequency' is inversely proportional to 'period') might provide a mechanism for explaining how the vibrations of one body might induce similar frequencies in another, some distance away, each displaying its own natural frequency, through a process we would call 'sympathetic' vibration or 'resonance'. Galileo would have been struck by examples of periodicity in nature, such as the regular motion of our Moon, of the moons of Jupiter (three of which he saw between 7-11 January 1610 and a fourth on the evening of the 12th, using his 'improved' telescope, and which later he christened 'the Medicean planets' after Grand Duke Cosimo II de' Medici) and of the planets themselves.

Galileo used pendulums extensively in his experiments for, once he had an understanding of their characteristics, he was able to use them as time measuring devices.

Pendulums are mentioned both in Galileo's Discourses Concerning the Two Chief World Systems, published 1632, and in his Discourses Concerning Two New Sciences.

We can summarize the major points he discovered about pendulums.

pendulums nearly return to their release heights

pendulums eventually come to rest; lighter ones come to rest sooner

the period is independent of the bob weight

the period is independent of the amplitude

the square of the period varies directly with the length

Some of Galileo's assumptions are true only under certain conditions.

The motion is affected by the resistance of the air. Galileo recognised this although he could not quantify it. Indeed, this would not become possible until the invention of effective vacuum pumps and the study of pendulums in evacuated containers.

In addition, the independence of amplitude on period is true only if the amplitude is very small when compared with the length of the cord. The swing's 'angle of arc' (see diagram) had to be less than 10°; only then would the pendulum seem to be isochronic.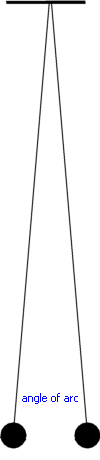

Although, in 1641, he turned his attentions to the design and construction of a clock regulated by a pendulum, he was by then blind. Milton describes how 'I found and visited the famous Galileo, grown old, a prisoner to the Inquisition for thinking in Astronomy otherwise than the Franciscan and Dominican licencers thought'. Copernicus' heliocentric model of the solar system (published in 1543 as De Revolutionibus Orbium Coelestium) found favour neither with the Catholic hierarchy nor with the Reformation's Martin Luther (14831546). Against the scientist who defended himself against the charge of impiety, saying that God reveals himself in Nature's actions, or as Galileo put it "Philosophy is written in that great book which ever lies before our eyes", Luther appears to argue that neither nature, history nor philosophy can reveal God and that man would be better not to pry into these things. However, Luther also wrote:

"... I am not of the opinion that all sciences should be beaten down and made to cease by the Gospel, as some fanatics pretend; but I would fain see all the arts, and music in particular, used in the service of Him who hath given and created them."

Much later, the remarkable Emanuel Swedenborg (1688-1772), would contemplate a reconciliation between religious dogma and practical science.

The Novum Organum was to transform scientific endevour, find itself applied to philosophy by René Descartes and to political theory by Bacon's sometime amanuensis Thomas Hobbes. The books of religion themselves should be subject to scientific scrutiny. The Reverend Thomas Burnett (1635-1715) author of Telluris theoria sacra, a courageous attempt to reconcile the Bible to the latest scientific theories, wrote:

"'Tis a dangerous thing to engage the authority of scripture in disputes about the natural world in opposition to reason; lest time, which brings all things to light, should discover that to be evidently false which we had made scripture assert."

While Spain's defaults under Philip II between 1559 and 1596 ruined the Catholic banking dynasties of Italy and south Germany, shifting the locus of financial power to Northern Europe, the attitude of the Catholic Church to the scientific method brought an end to scientific enquiry in Italy and, it is arguable, also contributed to moving the centre of European wealth creation from the Mediterranean world of thirteenth, fourteenth and fifteenth century Venice and Genoa to seventeenth century Amsterdam and eighteenth century London. Venice had for so long been a symbol of freedom and the pleasures of life. By the mid-seventeenth century, French practices began to insinuate themselves into the rigid Venetian tradition. Although composers from beyond the Alps such as Johann Rosenmüller, Johann Philipp Krieger and Johann Wolfgang Franck continued to come to Venice to learn its exclusive musical idiom, Venetian musicians began writing alla tedesca (in the German manner), perhaps seeking to please their new patrons, for, as far as instrumental music was concerned, these patrons were now almost exclusively foreign. The economic situation in Venice was deplorable: the illustrious music publishers were disappearing (Rosenmüllers Sonatas of 1667 were the last to be published by Vincenti, while Legrenzi s La Cetra collection was the only work printed in Venice in 1673), and the dwindling commissions and reduced honorariums, together with the lack of local patrons, were encouraging the immigration of musicians, particularly to Vienna and the court of the highly musical Emperor Leopold I and before long to places even further north.

When the Dutch Protestant Prince of Orange came to the English throne in The Glorious Revolution of 1688, Dutch political and commercial power was at its peak. England and Holland were to become the most urbanised and industrialised regions with 25% of the population living in towns and cities as opposed to 10% or less elsewhere. The wealth created by industrial advance, and the part played by science in supporting new technological innovations, fostered men with boundless self-confidence and burning ambition.

The first practical pendulum regulated clock was produced in late 1656 by the Dutch mathematician and physicist Christiaan Huygens, working closely with the clockmaker Salomon Coster in Amsterdam. Huygens was unusual because although Protestant and Dutch, he became secretary to the Paris-based Académie Royale des Sciences founded in 1666 with the encouragement of the notoriously intolerant Catholic monarch Louis XIV.

The first complete description of his new clock was published by Huygens in 1658 in his book Horologium with additional details published in 1673 in his Horologium Oscillatorium. Huygens was the first to show why a pendulum swinging through the arc of the circle is not actually isochronic. It only appears so when the length of the arc is quite short relative to its radius of curvature. In fact it is a curve called the 'cycloid' that is a 'tautochrone', i.e. when released from any point on the curve and moving along it only under the influence of gravity, a particle reaches the lowest point on the curve at the same time. The difference between the time of swing of a circular arc as opposed to that following a cycloid path is called, by horologists, 'circular error'. Huygen's published his discovery in Horologium. By building a clock with a long pendulum and a short swing the 'circular error' could be minimised, and so it was in the 'grandfather clock' which would became a commonplace within a few centuries.

Huygens, like Galileo, was the son of a musician. Huygens fils made a useful contribution to seventeenth century musical theory. His study of the 31-tone division of the octave, probably discovered in 1661, was described in Lettre touchant le cycle harmonique published in Histoire des Ouvrages des Scavans, Rotterdam (1691) and in Novus cyclus harmonicus (Leiden 1724). He explained how logarithms could be used to calculate the division of the octave, although the first to use logarithms for the calculation of interval sizes were Bonaventura Cavalieri (1639), Juan Caramel de Lobkowitz (1647), and Lemme Rossi (1666). He discussed several theoretical and practical advantages of the 31-tone division, the usefulness, as a solution to the problem of tuning keyboard instruments, of which he was at first sceptical. However, by 1669 he had constructed a keyboard based on the 31-tone division upon which he performed. This followed in a tradition of invented keyboard instruments that could preserve 'enharmonic distinction', an essential feature of scales based on ancient Greek tuning systems. The most famous of these was the archicembalo produced by the Italian composer Nicolà Vicentino (1511-1572), which incorporated six rows of keys.

Ref: Revolutions in Time by David S. Landes , Viking (revised edition) [2000]
Ref: Division of the octave into 31 equal parts
Ref: Logarithmic Interval Measures

Galileo conducted other experiments. Drawing a scraper across a series of parallel evenly spaced grooves cut into a plate, he confirmed that the distance between the grooves varied according to the pitch of the note produced; the greater the number of grooves over a certain distance, the higher the pitch of the note heard. He was able to reproduce, although in a completely different way, an observation already known to the ancient Greeks. They had discovered that two notes, one fifth apart, were produced from strings whose lengths bore the ratio 3:2. Galileo discovered that the number of lines spaced over a certain length that produced two notes, one fifth apart, also bore the ratio 3:2.

The relationship between frequency and pitch which Galileo hints at in his writings, was actually described more clearly by the Franciscan friar Marin Mersenne in his Harmonie universelle, contenant la théorie et la pratique de la musique, published in Paris in 1636-7, two years before Galileo's Discorsi. Mersenne measured the time of return of an echo, and arrived at a figure for the velocity of sound that was within less than 10% of the true figure.

Mersenne also made the first crude determination of the actual frequency of a note of a given pitch, 84 cycles per second, by observing the motion of a long heavy wire that moved slowly enough to be followed by the eye. From theoretical considerations, he could then calculate the frequency of a short, light wire, one that produced an audible sound.

Mersenne also discovered the following relationships:

for a string under constant tension, frequency varies inversely as the length;
for a string of constant length, frequency is proportional to the square root of the tension;
for given length and constant tension, frequency varies inversely as the square root of the mass/unit length.

These have been combined to produce the Mersenne-Taylor equation, named after Mersenne and the English mathematician Brook Taylor (1685-1731).

Mersenne defended the French philosopher Descartes (Descartes, himself, wrote on the theory of music; you will find a summary at Compendium Musicae), who had been a fellow student with him, and Galileo against theological criticism and struggled to expose the pseudo-sciences of alchemy and astrology. He continued some of Galileo's work in acoustics and stimulated some of Galileo's own later discoveries. He proposed the use of the pendulum as a timing device to Huygens.

Mersenne published translations into French of parts of Galileo's Dialogo, (Les mécaniques de Galilée; Paris, 1634), and of Galileo's Discorsi, (Nouvelles découvertes de Galilée, and Nouvelles pensées de Galilée sur les mécaniques; Paris, 1639). It is through Mersenne that Galileo's work became known outside Italy.

It is clear now that Galileo's discovery was made long before he published his description. Galileo's first notes on the subject date from 1588, but he did not begin serious investigations until 1602 so that his discovery predates Mersenne's. However, Mersenne was the first to actually measure the frequency of a vibrating string.

We know, both from his own diary and that of Samuel Pepys, that the English physicist Robert Hooke (1635-1703) carried out his own study of sound.

Pepys, making an entry in his diary for 8 August 1666, records a chance meeting with the famous scientist.

"Up, and with Reeves walk as far as the Temple, doing some business in my way at my bookseller's, and elsewhere, and there parted, and I took coach (having first discoursed with Mr. Hooke a little, whom we met in the street, about the nature of Sounds, and he did make me understand the nature of Musicall sounds made by Strings, mighty prettily; and told me that having come to a certain Number of Vibracions proper to make any tone, he is able to tell how many strokes a fly makes with her wings (those flies that hum in their flying) by the note that it answers to in Musique during their flying. That, I suppose, is a little too much raffined; but his discourse in general of sound was mighty fine)."

Ref: The Shorter Pepys by Robert Latham, Bell & Hyman Ltd. [1985]

Hooke's own diary (1675-76) tell us a little more about his thoughts on the subject:

"Saturday, January 15th - ...... To. Sir Chr. Wrens, Dr. Holder and I discoursed of musick, he read my notes and saw my designs, then he read his which was more imperfect. I told him but sub sigillo my notion of sound, that it was nothing but strokes within a Determinate degree of velocity. I told them how I would make all tunes by strokes of a hammer. Shewd them a knife, a camlet coat, a silk lining. Told then there was no vibration in a puls of sound, that twas a pulse propagated forward, that the sound in all bodys was the striking of the parts of one against the other and not the vibration of the whole. Told them my experiment of the vibrations of a magicall string without sound by symphony that touching of it which made the internall parts vibrate - caused the sound, that the vibrations of a string were not Isocrone but that the vibration of the particals was. Discoursd about the breaking of the air in pipes, of the musick of scraping trenchers, how the bow makes the fidle string sound, how scraping of metal, the scraping the teeth of a comb, the turning of a watch wheel &c., made sound. Compard sound and light and shewd how light produced colours in the same way by confounding the pulses"

Ref: Pandaemonium by Humphrey Jennings, Papermac [1995]

Hooke used a toothed cog wheel run against a piece of cardboard to generate sound, a method which is similar in some ways to Galileo's grooved metal sheet and scraper. Hooke is remembered today for Hooke's Law, which states that the force exerted by a spring is proportional to its extension multiplied by its 'stiffness' or 'elasticity'. Like his Dutch contemporary Huygens, Robert Hooke worked closely with a master clock-maker, Thomas Tompion. Tompion developed Hooke's invention, the balance spring, using it to regulate pocket watches. Hooke's Law was to form the basis of the mathematical theory of elasticity and thereby form the basis of the analysis of elastic vibrations associated with sound passing through bars and rods carried out principally by the mathematicians Leonhard Euler (1707-1783) and Daniel Bernoulli (1700-1782).

Euler was, in all probability, the most productive mathematician in history. He produced over half his work after he had become totally blind (1771). Much of his earlier work was assisted by Daniel Bernoulli, the latter giving up his chair in mathematics at St. Petersburg to Euler in order to return to Basel.

The work of the experimentalist Ernst Florens Friedrich Chladni (1756-1824), the father of German acoustics and inventor of the euphonium, who published Entdeckungen über die Theorie des Klanges (1787) and Die Akustik (1802), and the later theoretical work of Gustav Kirchhoff (1824-1887) established the theory of the vibration of plates.

The analysis of the vibrations of sound in flexible membranes, such as those in drum heads, was solved first by S.D. Poisson (1781-1840) and then, for circular membranes, by Rudolf Clebsch (1833-1872).

The dependence of a medium, whether gaseous, liquid or solid, for the transmission of sound was initially misunderstood. Athenasius Kircher (1602-1680) carried out experiments using a bell in a vacuum and a description appears in his book Musurgia Universalis sive Ars magna Consoni et Dissoni published in Rome in 1650. He concluded that air was not necessary to conduct sound. Either his pump was not very efficient or the sound was being transmitted in other ways. The first successful demonstration that the transmission of sound did require a medium was made in 1660 by the Anglo-Irish scientist Robert Boyle. Robert Hooke, acting as his assistant, had built a much improved vacuum pump. Repeating Kircher's experiment, suspending a bell in an glass jar, and removing the air from within the jar, he saw that although the clapper could still be seen striking the bell, he could hear no sound. In other experiments, Boyle also established the law that still bears his name, that the pressure of a fixed quantity of gas varies inversely as its volume.

The English mathematician, physicist and alchemyst, Sir Isaac Newton published the first significant mathematical treatment of the theory of sound in his Philosophiae Naturalis Principia Mathematica published in 1687 at the bidding of his friend and colleague Edmund Halley. Newton carried out the major part of his scientific work in secret and was slow to publish his results. In his 1956 Halley Lecture, given on the occasion of the tercentenary of Halley's birth, Professor Dingle wrote:

'We cannot doubt that without Halley there would have been no Philosophiae Naturalis Principia Mathematica. To quote de Morgan, "but for him, in all human probability, that work would not have been thought of, nor when thought of written, nor when written printed ..." Details must be forgone. I can only say that in the year 1684, when Halley was 27, the question agitating the minds of the mathematically inclined members of the Royal Society was whether Kepler's laws required an inverse square law of gravitation; several had guessed that this must be so, but no-one was known to have proved it. Four years earlier Hooke had tried to draw Newton out on the subject, and had been snubbed for his pains. Halley at once went to Cambridge, invaded the cherished privacy of Newton who was half as old again as himself, and learned that Newton had solved the problem long before but had mislaid the papers. Realising the overwhelming importance of the question, Halley repeated his visit, wheedled Newton into repeating his proof and developing its implications, and received from him the first Book of his immortal volume in 1686. The Royal Society agreed to print it, but later appeared to regret the expense. Halley, who seems to have been alone in perceiving that all the money in the Mint was negligible compared with the value of Newton's work, offered without argument to pay for it himself. Two further Books followed, and Halley accepted the cost of printing these also. The whole work was published about mid-summer, 1687, with an untypically generous tribute from Newton to Halley in the Preface and a eulogy of Newton in Latin hexameters by Halley.'

Newton reasoned that the propagation of sound through any fluid depended only on measurable physical properties of the fluid, such as elasticity and density. Further, he calculated from theoretical considerations the velocity of sound in air. Newton's analysis was incredibly ad hoc. He used Galileo's ideas for the particles in the medium through which the sound travels, which "are always accelerated or retarded according to the law of the oscillating pendulum".

Newton wanted his model to match the velocity of sound supplied by Derham, who had presented the figure merely as the average of a large number of measurements. To get his model to fit the observed value he assumed that air contains vapor in the quantity of 10 parts to 1 and that vapor does not participate in the sound vibrations, a wholly arbitrary idea, resting on no empirical foundation whatever. In addition, his use of the "crassitude" of the air particles to raise the calculated velocity by more than 10 percent has been called by some modern commentators 'nothing short of deliberate fraud'. His result was erroneous because he had assumed any local changes in the temperature of the gas caused by the change in pressure as the sound wave passed through the medium would be short-lived and could be ignored. In 1816-17, Laplace, while recognising Newton's stupendous achievement in deriving an estimate of the speed of sound from 'first principles', suggested that the changes in pressure are adiabatic, that the local temperature is raised and heat does not have time to dissipate into the surrounding gas. For this reason, the velocity of sound would be higher than that calculated on the basis of Newton's model without its attendant 'fudge' factors. Using his new formula, Laplace was able to match the measured velocity of sound.

Ref: Isaac Newton The Last Sorcerer by Michael White, Fourth Estate [1998]
Ref: Newton and The Velocity of Sound
Ref: The Speed of Sound

The French philosopher Gassendi (1592-1655) proposed that sound is due to a stream of fine invisible "particles" emitted by the sounding body, their speed being the velocity of sound and their emission rate (number emitted per unit time) being the frequency. This alternative to the 'wave theory' mirrored the duality underlying the physics of optics even today. The corpuscular theory of the constitution of matter led Newton to propose that light too was 'corpuscular' because it did not 'bend' around corners. Diffraction was then not understood. Huygens and others believed light to have an inherently 'wave-like' behaviour.

For both Newton and Huygens, sound waves provided the conceptual framework for all their more general theories of waves. Newton writes to Mr. Oldenburgh on the analogy of nature:

"I suppose that as bodies of various sizes, densities, or tensions, do by percussion or other action, excite sounds of various tones, and consequently vibrations in the air of various bignesses; so, when the rays of light, by impinging on the stiff refracting superficies, excite vibrations in the aether, those rays, whatever they are, as they happen to differ in magnitude, strength or vigour, excite vibrations of various bignesses; the biggest, strongest, or most potent rays, the largest vibrations, and others shorter, according to their bigness, strength, or power; and therefore the ends of the capillamenta of the optic nerve, which front or face the retina, being such refracting superficies, when the rays infringe on them, they must there excite these vibrations; which vibrations (like those of sound in a trumpet) will run along the aqueous pores or crystalline pith of the capillamenta, through the optic nerves into the sensorium (which light itself cannot do) and there, I suppose, affect the sense with various colours, according to their bigness and mixture; the biggest with the strongest colours, reds and yellows; the least with the weakest, blues and violets; the middle with green, and a confusion of all, with white; much after the manner that in the sense of hearing nature makes use of aërial vibrations of several bignesses, to generate sounds of divers tones; for the analogy of nature is to be observed! And, further, as the harmony and discord of sounds proceed from the proportions of the aërial vibrations, so may the harmony of some colours, as of a golden and blue, and a discord of others, as of red and blue, proceed from the proportions of the aetherial. And possibly colour may be distinguished into its principal degrees: red, orange, yellow, green, blue, indigo and deep violet, - on the same ground that sound within an eighth is graduated into tones."

When, in 1690, Huygens used his wave theory to explain the 'polarisation' of the two sets of rays produced when light is double refracted by crystals of Iceland spar, a property first observed by Bartholinus of Copenhagen in 1669, Newton showed that Huygens' analysis was deficient because 'longitudinal' waves, which Huygens used because they are analogous to sound waves, could not explain the observed effect. In fact, had Huygens employed 'transverse' waves rather than 'longitudinal' waves he could have overcome Newton's objections. In the nineteenth century, the ray concept was adopted to explain particular acoustic phenomena, but it was assumed that the method offered only an approximation to the results that would have been obtained, although with considerably greater effort, from the wave theory of sound.

Ref: Analogy in Ancient Greek Thought
Ref: Analogy in Patristic and Medieval Thought

British science fell completely under the spell of Newton. Newton's style of working, in 'splendid isolation' in Cambridge, became the accepted 'working model' for the scientific establishment for many generations after his death. In the search for political stability after Cromwell's Commonwealth, 'The Cause too good to have been fought for', religion was cleansed of Puritan 'enthusiasm' (one calls to mind the words of the Cambridge Platonist, Benjamin Whichcote (1609-1683): 'The good nature of a heathen is more God-like than the furious zeal of a Christian') and science purged of politically dangerous ideas. The scientific establishment, made up of ivory-towered academics, landed gentry and senior clerics became sterile and remote. This tendency had always been present in Britain's premier scientific body, the Royal Society. John Graunt, the author of Natural and Political Observations made upon the Bills Of Mortality first published in 1662, was a tradesman, a purveyor of "notions" such as buttons and needles. His book was immensely popular, appearing in at least five editions, and influential. It established the use of probability theory and statistics in the study of human populations. The King, Charles II, proposed Graunt for membership of the Royal Society, but the member's unenthusiastic response prompted the King to write that 'if they found any more such Tradesmen, they should be sure to admit them all, without any more ado'. In the 1830s, the Royal Society entered a period of bitter division and self analysis, revolving around the question who ran science; the aristocrats whose money bought them influence and prestige, or the scientists whose ingenuity, committment and genius had advanced human understanding and potential.

In addition, a last ditch attempt was made in England to harness science to religion, by commissioning, under the terms of the will of the 8th Earl of Bridgewater, a series of essays designed to demonstrate 'The Goodness of God as Manifested in the Creation'. Unfortunately, progress in the science of geology had begun to undermine the chronology of the Creation as set out in the Bible and futile attempts at a reconciliation by the authors of the treatise on geology and mineralogy led the scientist and writer Mary Somerville to observe that 'facts are such stubborn things'.

Practical scientific advancement in late eighteenth and early nineteenth century Britain sprang mainly from non-Conformist bodies like the Warrington Academy, founded in 1757, where Joseph Priestley taught, and local societies such as The Manchester Philosophical Society and The Lunar Society of Birmingham (1775 - c. 1791) all based in the thriving, thrusting industrial heartland of England. Amongst its members the Lunar Society could boast James Watt, the greater 'improver' of the steam engine, Matthew Boulton, Watt's business partner, James Keir, a pioneer of the chemical industry, William Murdoch, engineer and discoverer of gaslight, Joseph Priestley, who discovered oxygen, Dr. William Withering, who discovered the action of digitalis on the heart, Erasmus Darwin, eminent biologist and grandfather of Charles Darwin, Josiah Wedgwood, Charles Darwin's other grandfather and a potter, and Richard Edgeworth, whose daughter Maria, like her father before her, was influenced by the ideas of Jean-Jacques Rousseau and became a writer on educational reform. In London, Michael Faraday, a member of the non-Conformist Sandemanian church, continued and developed public lectures on scientific topics at the Royal Institution, where in 1825 he was appointed Director of The Laboratory, by instigating a series of Friday Evening Discourses, the first given by him on the subject of 'Caoutchouc', the natural form of rubber and later in 1828 on 'The Nature of Musical Sound'.

Ref: James Watt and The Lunaticks of Birmingham by Adam Hart-Davis
Ref: John Graunt - Observations On The Bills Of Mortality
Ref: 'Faraday - the life' by James Hamilton; published by Harper Collins

When Richard Arkwright, the inventor of one type of spinning machine, was forced to resort to law to protect one of his patents, his counsel described matters thus.

"It is well known that the most useful discoveries that have been made in every branch of art and manufactures have not been made by speculative philosophers in their closets, but by ingenious mechanics, conversant in the practices in use in their time, and practically acquainted with the subject-matter of their discoveries."

Ref: Puritanism and Revolution by Christopher Hill, Peregrine Edition, Penguin [revised 1984]
Ref: The Western Intellectual Tradition by J. Bronowski & Bruce Mazlish, Penguin [revised 1970]

Of course, scientists and mathematicians of this period, like those before and after them, were practical men.

Galileo designed and built a special calculator, his 'Military Compass', which, among other things, extracted square roots. The telescope, which he did much to make practical both as a terrestrial and a celestial instrument, was used by Venetian brokers to spot incoming ships so that they could advantage themselves on the trading floor of the Rialto. Olaf Roemer's discovery that the speed of light was finite and could be measured arose directly from a suggestion of Galileo, that the moons orbiting Jupiter might be used by mariners as an astronomical 'time-keeper', an extra-terrestrial clock.

Robert Hooke invented the universal joint and the iris diaphragm (possibly also the anchor escapement used to improve the timekeeping of pendulum clocks and, as we saw earlier, the balance spring) and was as important in the rebuilding of London following the Great Fire of 1666 as Sir Christopher Wren, himself an astronomer and mathematician as well as an architect. The Monument which marks the spot where the Great Fire started was designed by Hooke.

Newton invented his reflecting telescope, taken from an idea of Gregory (1663) and Zucchi, to get around the problems of chromatic aberration in refracting telescopes. His work with telescopes was to prompt him to consider the properties of light in a more general way and led to his great work 'Opticks' (published in 1704, the year following the death of Robert Hooke). The whole of astronomy including the work of Ptolemy, Copernicus and Kepler was driven by a need to perfect and correct calendars and to improve the accuracy of astrological charts and horoscopes, still retaining in the late seventeenth century their importance in everyday life as described six centuries earlier by the Chinese administrator and diplomat Su Sung.

"Those who make astronomical observations with instruments are not only organising a correct calendar so that good government can be carried on but also predicting good and bad fortune and studying the resulting gains and losses."

Huygen began his career striving to improve the two most important navigational tools of the seventeenth century, the telescope and the clock.

Many a leading mathematician of the sixteenth, seventeenth and eighteenth centuries was employed to make or break diplomatic, commercial and military codes. One thinks of John Dee in Elizabethan England, Francisco Vieta solving Spanish codes for the King Henry IV of France, John Wallis solving Royalist codes for the Roundheads, Thomas Young deciphering Egyptian hieroglyphics and more latterly Sir Alfred Ewing heading the naval decoding department in the First World War and Alan Turing working at Bletchley Park during the Second World War. John Graunt's application of the 'new' science of statistics provided an estimate of the proportion of the population of fighting age.

Music as an art form touched the lives of many of the scientists we have mentioned above. Indeed, we have alluded to both Galileo and Huygens as executants. Samuel Pepys, elected President of The Royal Society on 30 November, 1684, set out his valediction in a letter written on 5th November, 1700.

"Musik, a science peculiarly productive of a pleasure that no state of life, publick or private, secular or sacred; no difference of age or season; no temper of mind or condition of health exempt from present anguish; nor, lastly, distinction of quality, renders either improper, untimely or unentertaining."

And yet for some, the business of music held little attraction. On 18th April 1720, the Reverend William Stukeley reports in his diary:

"He [Sir Isaac Newton] said he never was at more than one Opera. The first Act he heard with pleasure, the 2nd stretch'd his patience, at the 3rd he ran away."

The eminent scientific philosopher was not merely an object of amusement amongst his fellow creatures. Many a well-meaning amateur tried to apply Newton's "Laws" to other areas of human experience; for instance Francesco Algarottis Isaac Newtons Philosophy Explained for the Use of the Ladies (1739)

"I cannot help thinking, said the Marchioness, that this proportion in the squares of the Distances of Places, or rather of Times, is observed even in Love. Thus after 8 Days Absence Love becomes 54 times less that it was the first Day and according to Proportion it must soon be entirely obliterated; I fancy there will be found, especially in the present Age very few Experiences to the contrary."

According to Jean-Jacques Rousseau, in his Dictionnaire de Musique printed in 1768, the French physicist, Joseph Sauveur (1653-1716) invented the word l'acoustique in 1697 to describe the 'science of sound'; the English form is acoustic. However, Narcissus Walsh, presented a paper to the Dublin Society in 1683, entitled: An introductory Essay to the Doctrine of Sounds, containing some proposals for the Improvement of Acoustick suggesting that the word was more widely used than Rousseau had realised.

Sauveur and the English mathematician John Wallis (1616-1703) first described the behaviour of a vibrating string in terms of nodes (where the string was at rest) and loops (where the amplitude of displacement was a maximum). Today, we use the term 'antinode' instead of 'loop'. Sauveur was certainly the first to apply the terms 'fundamental' and 'harmonic' to integer multiples of any particular frequency and to suggest that a vibrating string produced its fundamental and harmonics at the same time, these words appearing in his paper Système général des Intervalles et son application à tous les Instrumens de Musique in the Mémoires de l'Académie Royale des Sciences, Paris in 1701 and other papers and communications written between 1697 and 1713.

Ref: Collected Works of Joseph Sauveur (Paris 1700-1713) [1984]

The joint invention of the calculus by Newton and Leibniz advanced the use of differential equations as a means of expressing the behaviour of physical systems. The notational advantages that came from Leibniz's formulation gave European mathematicians a considerable advantage over those working in England who still clung to Newton's more arcane notation.

Brook Taylor produced the first strictly dynamical solution of the problem of the vibrating string. It was published in Philosophical Transactions in 1715, and was the precursor to the celebrated paper by Daniel Bernoulli, published by the Berlin Academy in 1755. In the latter paper, Bernoulli sets out his superposition principle. His analysis of the motion of a vibrating string was that the displacement of every point on the string was the algebraic sum of the displacement produced by the fundamental and all its harmonics. This principal found a more universal application in the hands of the French mathematician Baron Jean Baptiste Joseph Fourier (1768-1830) who used it in his 'Analytical Theory of Heat' published in 1822 to express a mathematical function as an infinite series of sines and cosines.

Bernoulli's approach was finally improved upon by the mathematician Joseph Louis Comte de la Grange (1736-1813) who in an extensive paper entitled Recherches sur la Nature et la Propagation du Son published by the Turin Academy in 1759, produced the first wholly analytical solution to the theory of vibrating strings. la Grange, or Lagrange as his name is more usually written today, was probably one of the greatest figures in eighteenth century mathematics. It was he who first suggested that the musical properties of violins, flutes and trumpets could be understood using his new vibration theory. He 'broke' the string up into a finite number of equally spaced particles of identical mass. He considered the motion of this system and was able to establish many independent frequencies, in fact, as many frequencies as there were particles. By passing from the sum of a finite number of particles of finite mass, to a system of infinite particles of correspondingly small mass, he found the allowed frequencies to be the harmonic frequencies of a stretched string. Lagrange's paper also considered a theoretical method for approximating the harmonic frequencies of open and close pipes extending again earlier important work on the vibration of air in cylindrical tubes by Daniel Bernoulli, published as Recherches Physiques, Mécaniques et Analytiques, sur le Son et sur les Tons des Tuyaux d'Orgues différemment construits in the Mémoires de l'Académie Royale des Sciences, Paris, in 1762.

One should not underestimate the importance of the work of mathematicians like Daniel Bernoulli, his brother Jacob (sometimes known as James), Brook Taylor, Lagrange and others, who as they applied themselves to specific problems in mathematical physics, including those in the area of 'acoustics', were engaged in a fundamental study of differential equations, including the search for methods for finding their solutions. These studies would find themselves applied, in due course, to problems ranging from celestial dynamics to cable theory. Although Newton had solved the first differential equation in 1676, Lagrange's work on the form of the vibrating string, a problem initially discussed by Euler and d'Alembert, provided a new method, the 'variation of parameters', for finding solutions to the first recognised partial differential equation, which was actually of second order, as well as to linear equations of any order.

d'Alembert and the German physicist Georg Simon Ohm worked to deepen understanding of pitch and quality of sound produced by a particular musical instrument, what we call 'timbre', and the speed and nature of transmission of sound in various media.

d'Alembert's method for solving the problem of the vibrating string, which treats the string as a continuous medium, and derives and solves the differential equation of motion, what we would call the 'wave' equation, is that most commonly used in high school physics texts today. The greatest contributors to acoustics in the late nineteenth century were Hermann von Helmholtz (1821-1894) and J.W.S. Rayleigh (1840-1919). Their masterworks Die Lehre von den Tonempfindungen als Physiologische Grundlage für die Theorie der Musik by Helmholtz (available in an English translation entitled Sensations of Tone by A.J. Ellis) and The Theory of Sound by Lord Rayleigh repay study even today.

Variations in sound called 'beats' were studied by Sauveur who recognised them to arise as 'difference tones' between the fundamentals of two pipes imperfectly tuned to a unison. 'Beating' is best heard when the difference is small, when the beats can be counted by an experienced observer as a series of distinct pulses rather than being heard as just a third note. Beats between fundamentals are called the 'unison beats'. Others recognised that 'beating' might occur between 'harmonics' of two different pipes where the difference between a harmonic of one pipe approached that of a second pipe. These are called 'overtone beats'. A third type of beat called the 'beat of imperfect consonance' we will cover later.

It was clear from very early times that sound travelled noticeably slower than light. Robert Grosseteste (c. 1168-1253), the real founder of the tradition of scientific thought in mediaeval Oxford, espoused a theory of science based on Aristotle's distinction between knowledge of a fact and knowledge of the reason for the fact. So, for example, geometry could give an account of an optical phenomenon, but it could not explain why it happened. His contemporary, Roger Bacon (c. 1214-1294), asserted that the propagation of light was not a flow like water, but a kind of pulse as in sound. Bacon noted that light travelled much faster than sound, for if someone at a distance is banging with a hammer, we see the blow before we hear the sound.

Although Aristotle had proposed that sound was carried by the motion in the air, the absence of detectable motion led others, among them the early seventeenth-century French natural philosopher and astronomer, Pierre Gassendi, to propose that sound was propagated in a stream of fine, invisible particles from the original source to the ear. Gassendi, through a study of the works of Epicurus (341-270 BC), rediscovered the ideas of Democritus who, two generations before Aristotle, stated that, "colour exists by convention, sweet by convention, bitter by convention, in reality nothing exists but atoms and the void". Otto von Guericke (1602-1686) also disagreed with Aristotle, observing that sound travelled better in still air than when there was a wind. Even though there might be disagreement as to the mechanism by which sound travelled, by the seventeenth century, experimentalists, including Gassendi, Mersenne, Borelli, Viviani and Branconi, were already trying to measure its velocity. The earliest estimates varied because there was only a dim awareness that temperature, motion of the air and humidity influenced the result. Gassendi showed that velocity was independent of the pitch of the sound, which contradicted Aristotle but explained why musical performances heard over a long distance remained coherent. The first precise outdoor measurement was carried out in 1738, under the direction of the Academy of Sciences of Paris, using cannon fire. Corrected for temperature their result, 332 metres/sec, compares well with the modern value of about 331.36 metres/sec.

Others, including Chladni and J. B. Biot (1774-1862), measured the velocity of sound in solid media and through liquids.

The 19th century was primarily a period of experimental development. Experimental demonstrations to prove the mathematical work of the previous century were numerous and ingenious. The first accurate measurements of the speed of sound in water were made in 1826 by the French mathematician Jacques Sturm, and throughout the century numerous experiments were made determining the speed of sound of various frequencies in various media with extreme accuracy. The fundamental law that the speed is the same for sounds of different frequencies and depends on the density and elasticity of the medium was determined in these experiments. The stroboscope, the stethoscope, and the siren were all used in the study of sound during the 19th century.

The standardization of pitch occupied much attention in the 19th century. The first suggestion for a standard had been made about 1700 by the French physicist Joseph Sauveur, who proposed C equals 256Hz, where Hz is one cycle per second, a convenient standard for mathematical purposes. The German physicist Johann Heinrich Scheibler made the first accurate determination of pitch corresponding to frequency and proposed the standard A equals 440Hz in 1834. In 1859 the French government decreed that the standard should be A equals 435Hz, based on the research of the French physicist Jules Antoine Lissajous. This standard was accepted in many parts of the world, including the United States, until well into the 20th century.

The association of the physical analysis of sound with the psychological aspects began as a serious study in the hands of Helmholtz. The human dimension affects our appreciation of tone, pitch and timbre and is something we need to appreciate to distinguish between mechanical data from physical instruments and what we actually hear or believe we hear. For example, Karl Ernst von Baer (1860), introduced a characteristic time constant, about 55 msecs, which he argued represented the time it took a human being to become conscious of a particular sensory impression. A good summary of this work and more besides is to be found in Music, Sound and Sensation by Fritz Winckel published by Dover, 1967, from which we have taken the following extract.

"These remarks should prove sufficient to show how in the human world principles of music aesthetics are determined by a physiological constant; the boundaries of the tone spectrum, the speed with which tones follow each other, the evaluation of the tone colour, the 'space' perception of sounds and the ability to determine the direction of the sound source."

One must consider also the way in which the environment influences the way sound is projected from the source to the listener. The pioneer in this field was the American physicist Wallace Clement Sabine (1868 - 1919), called 'the father of architectural acoustics'. Many of his important papers have been republished by Dover (1964) under the title Collected Papers on Acoustics. The variation of sound absorption with frequency which is different for different materials has a direct effect on the acoustics inside buildings as does the presence or absence of an audience. Internal reflection too must be considered and the way it can enhance or reduce the quality of speech or music.

During the 19th century the telephone, the microphone, and the phonograph, all of which were useful for further study of sound, were invented. In the 20th century, physicists for the first time had instruments that made possible simple, accurate, quantitative study of sound. By means of electronic oscillators, waves of any type may be produced electronically, then converted into sounds by electromagnetic or piezoelectric means. Conversely, sounds may be converted into electrical currents by means of a microphone, amplified electronically without distortion, and then analyzed by means of a cathode-ray oscilloscope. Modern techniques permit extremely high-fidelity recording and reproduction of sound.

Military necessity in World War I led to the first use of sound for underwater detection of vessels; sound is now also used for studies of ocean currents and layers, and for sea-bottom mapping. In addition, ultrahigh-frequency sound waves are now used in a wide range of technical and medical applications.

Refs: history of the science, science of sound and its modern day applications
A Treatise on The Flute by R.S. Rockstro, 2nd Edition (1928) reprinted by Musica Rara [1967]
The Theory of Sound by J.W.S. Rayleigh, 2nd Edition (1894) reprinted by Dover Publications [1945]
Links to University Departments undertaking Acoustical Research
Sites of Interest to Acousticians
Eighteenth Century Resources - including Music, Mathematics and Science

How far, one might ask, had physics progressed from the time when Sir Francis Bacon wrote in De Interpretatione Naturae, the passage we quote above. Rayleigh's Presidential Address to the British Association in Montreal in 1884 is an eloquent summary of the achievements both of his lifetime and of the previous two hundred and sixty years.

"Without encroaching upon grounds appertaining to the theologian and the philosopher, the domain of natural sciences is surely broad enough to satisfy the wildest ambition of its devotees. In other departments of human life and interest, true progress is rather an article of faith than a rational belief; but in science a retrograde movement is, from the nature of the case, almost impossible. Increasing knowledge brings with it increasing power, and great as are the triumphs of the present century, we may well believe that they are but a foretaste of what discovery and invention have yet in store for mankind. ... The work may be hard, and the discipline severe; but the interest never fails, and great is the privilege of achievement."

Not everybody takes science or its ally mathematics quite so seriously. In 1952 a music critic of The Times wrote

`At Redbrick they treat mathematics as an instrument of technology; at Cambridge they regard it as an ally of physics and an approach to philosophy; at Oxford they think of it as an art in itself having affinities with music and dancing'.

We conclude this survey by quoting from the University of New South Wales, Physics Department's web page on Acoustics where they consider the future of this exciting branch of the physical sciences.

What is the future of Acoustics?

Communications

With the rapid development of computers it is already possible to communicate directly with them by voice control and to make them reply using sounds. Devices which routinely recognise and simulate speech will become increasingly common in the next few decades. Voice transmission over long distances by cable or microwave links are other areas where current technology is making rapid progress.

Underwater Acoustics

Detecting a submarine underwater, tracking schools of fish, determining the average temperature of large tracts of ocean to check on global warming are but a few applications of this expanding field.

Ultrasonics

Detecting flaws in aircraft structures or in the welds of a huge oil rig are just two applications of ultrasonics. In medicine, similar principles apply to the detection of tumours in the body or of imaging an unborn baby. Ultrasonic baths are commonly used to clean contamination from sensitive surfaces, while ultrasound can also be used to cut holes in extremely hard materials where an ordinary drill would not penetrate.

Architecture

New and improved sound insulating materials are continually being included in modern architectural structures to produce quieter living environments and more pleasing concert halls and other entertainment venues.

Life Studies

Bionic ears which can allow some deaf people to regain their hearing are already being utilised, but there is much more progress yet to be made in this field. How do birds or dolphins communicate using sound, what effects does changing the nature of a forest have on the ability of birds to communicate are areas under current study.

Acoustics is already playing a significant role in modern communities and there is tremendous scope for enthusiastic people to play an important role in continuing these developments by mastering and applying the principles of acoustics.