|
Pitch
::

|
Key word:
pitch |
| 1 |
Pitch
We reproduce below Ellis' famous table entitled History of Musical Pitch which demonstrates the various pitches used at different times in different places.
Why did pitch vary so much even during the same period in history?
One obvious answer is that there was no universal pitch standard. Before the widespread use of keyboard instruments, most serious music in the Middle Ages, both sacred and secular, was sung. The monochord, used to check intervals, was too rudimentary a device to be of use as a pitch reference.
Even into the sixteenth century, the pitch for a cappella performance was set not by the notated parts but rather, as Ludovico Zacconi writes in his Prattica di Musica, pub. Venice (1596), "to have regard for those who are to sing, that they be at ease with the pitch, neither too high nor too low." Something similar continues to this day, for example, in Sacred Harp singing where tunes are sung in relative pitch, rather than at an absolute pitch derived from A=440Hz.; referred to as " Pitch of Convenience", a long standing tradition as can be seen from directions for setting the first note from the Bay Psalm Book*.
(* For more on this topic see here)
Once we reach an era where pitch and tuning were anchored to that of a pre-tuned keyboard instrument, any freedom all but disappeared. Where musicians performed in a band, an orchestra, at court, in the opera house or in a church they would have to cope with several different working pitches. For stringed and keyboard instruments the solution was to retune the instrument. It is said that Isabella d'Este (1474-1539) considered stringed instruments, such as the lute, superior to winds, which were associated with vice and strife. Maybe for wind instruments this association reflected their inability to cope with changes in the pitch, a problem that could be solved only by purchasing completely new instruments when moving from place to place, venue to venue, or by working from parts specifically transposed to take account of the difference in pitch. Once the Hotteterre family had redesigned woodwind instruments to be made in sections rather than in a single piece, transverse flutes could be made with extra sections which, if longer, lowered or, if shorter, raised the pitch of the instrument. An adjustable plug in the head section was used to correct the tuning and speaking properties of the flute as the middle sections were exchanged. Brass instruments were also made with extra crooks, small lengths of tubing called corps de réchange, which could be fitted to the instruments to change their pitch. Quite apart from the problems of starting at the same pitch, there was also the reality of playing together as the ambient temperature changed. If the ambient temperature rises, the pitch of stringed instruments, like harpsichords, lutes and violins, drops, while that of wind and brass instruments rises. Played together, the two groups move in opposite directions and what might start out well enough would soon become increasingly strained particularly if the instruments were being played in small concert halls, theatres or opera houses. Churches were less of a problem because they tended to remain cool whatever the weather outside. Sir John Hawkins, writing in 1776, tells us that the tuning fork, originally called the 'pitch-fork', was invented in 1711, by John Shore, a trumpeter in the band of Queen Anne. It provided the first and, until the advent of electronic meters, the most trustworthy pitch-carrier, and was in every way superior to the 'pitch-pipe' about which the French philosopher Jean-Jacques Rousseau (1712-1778), writing in 1764, noted "the impossibility of being certain of the same sound in two places at the same time".
As an interesting aside, in Korea, pitch was set using resonant stones, called kyong-sok, which whatever the temperature or the humidity would, when struck, produce a reliable pitch reference. Until comparatively recently, most musicians and scientists, set the note C rather than A. Today, we tune our instruments to internationally agreed pitch standards set for A (actually a' or la4 ) although it should be pointed out that in a world where equal temperament is widely used, setting A also uniquely sets every other note of the chromatic scale, including C.
The most widely used standard, first proposed at the Stuttgart conference of 1838, but not properly established until 1938 in Britain and in 1939 by the International Organization for Standardization (ISO), is a'=440 Hz. Hz is an abbreviation of the name of the German physicist, Heinrich Hertz (1857-1894), and is a unit of frequency equivalent to one cycle per second. Neither the Stuttgart (1838), the ISO conference (1939) nor its successor held in London in October 1953, was completely successful in setting an internationally agreed pitch. These points are discussed in more detail in A Brief History of Musical Tuning by Jonathan Tennenbaum
Sound is a wave associated with the transmission of mechanical energy through a supporting medium. It can be shown experimentally that sound cannot travel through a vacuum. The energy available in a sound wave disturbs the medium in a periodic manner. Periodicity is important if a sound wave is to carry information. In air, the disturbance propagates as the successive compression and decompression (the latter sometimes called rarefaction) of small regions in the medium. If we generate a pure note and place a detector (our ear, for example) at a point in the surrounding medium, a distance from the source, the number of compression-decompression sequences arriving at the detector during a chosen time interval is called the frequency. The time interval between successive maximal compressions is called the period. The product of the frequency and the wavelength is the velocity. You are probably aware that the speed of sound is far lower than the speed of light (the speed of light is 299,792,458 metres per second). When, in the middle of a thunder storm, the flash of lightning is followed, noticeably later, by a clap of thunder, we take ever greater comfort the longer the delay. At ground level and at 0° C. the speed of sound is approximately 331.5 metres per second (c. 1,194 km or 760 miles per hour). This is approximately equivalent to 1 mile every 5 seconds (or very roughly 1 km every 3 seconds). The wavelength of the note we call a'=440 Hz proves to be about 753 mm (approximately 30 inches). Bats, who use a signal of about 35,000 Hz (usually written 3 kHz) to search for food, switch to higher frequencies (40-90 KHz) in order to more accurately locate their prey. At these higher frequencies the wavelength is in the range 8-4 mm.
It has long been established, and was described thus by Rayleigh, "that within certain wide limits the velocity of sound is independent, or at least very nearly independent, of its intensity, and also of its pitch (that is, its rate of vibration)". In general terms this must be the case otherwise how could music remain coherent even when it has travelled some considerable distance from performer to listener. However, high frequency sounds do lose more energy than do low. This is one of the reasons why we can tell if a known sound is distant: it has lost more high frequency energy, and this contributes to the 'muffled' sound (see FAQ in music acoustics).
The credit for the first correct published account of the vibration of strings is usually given to Marin Mersenne (1588-1648) although Galileo Galilei (1564-1642) published a remarkable discussion of the vibration of bodies in 1638, derived from his study of the pendulum and of the relationship between pendulum length and frequency of vibration. Although this appeared two years after Mersenne published his Harmonicorum Liber, Galilei's discoveries pre-date those of Mersenne. Wallis (1616-1703) and Joseph Sauveur (1653-1716) noticed that along a vibrating string there are points where there is no motion and others where the movement is particularly violent. Sauveur coined the term 'node' for the former and 'loop' for the latter, although, today, we use the term 'antinode' instead of 'loop' and also suggested the terms 'fundamental' and 'harmonic', applied to frequencies that are integer multiples of a particular frequency. In the discussions that follow, we have adopted the convention that the fundamental is the first harmonic although, in some books, the first harmonic is the name given to the second, not the first, note in the harmonic series. By the sixteenth century, it was clear that the interval relationships between notes, applied to the frequencies of those notes, was identical to the ratios discovered by the Greek from their study of the sounding length of vibrating strings. We have prepared an article entitled the Physics of Musical Instruments - A Brief History to which you may wish to refer for further details on this topic. Our appreciation of pitch stability has changed as some instruments notorious for their pitch and tuning instability have been replaced with instruments that are much more stable. For example, modern electronic instruments are almost entirely insensitive to changes in ambient temperature, while even the humble modern piano, with its full metal frame, is a much more stable platform than the half metal half wood framed pianos made three quarters of a century ago, or than the harpsichords, clavichords and spinets made three centuries earlier. Similarly, the relative uniformity of pitch standards around the world, makes it much easier for the modern musician to travel and perform abroad.
However, one must not ignore that fact that 'being' sharp or flat may have its cause outside the immediate mechanics or physics of the instrument upon which one is playing. James Holland, in his book Percussion (Yehudi Menuhin Music Guides, pub. Kahn and Averill, London), writes of the problems when playing the xylophone in unison with violinists in the higher registers.
|
It is, I believe, a fact that most people tend to hear sharp in the upper octaves, and of course violinists are known to play sharp in the upper registers, where the fingering becomes so close that it becomes almost impossible to play rapid passages without this tendency. These two factors together have led to many professionals' having the xylophone tuned 'brighter', or very slightly sharp, in the upper octaves. Even so, the xylophonist, with his instrument of fixed pitch, will fequently find himself flat compared to the violins in any very high unison passages. In these instances there is nothing that can be done, apart from trying to make the violins section aware of their tendency to be too high - no easy matter!
|
Indeed, the perception of pitch is a complicated process as this extract from Pitch (music) explains:
|
The note A above middle C played on any instrument is perceived to be of the same pitch as a pure tone of 440 Hz, but does not necessarily contain a partial having that frequency. Furthermore, a slight change in frequency need not lead to a perceived change in pitch, but a change in pitch implies a change in frequency. In fact, the just noticeable difference (the threshold at which a change in pitch is perceived) is about five cents (five hundredths of a semitone), but varies over the auditory range and is more precise when the two pitches are played simultaneously. Like other human stimuli, the perception of pitch also can be explained by the Weber-Fechner law.
Pitch also depends on the amplitude of the sound, especially at low frequencies. For instance, a low bass note will sound lower in pitch if it is louder. Like other senses, the relative perception of pitch can be fooled, resulting in "audio illusions". There are several of these, such as the 'tritone paradox', but most notably the 'Shepard scale', where a continuous or discrete sequence of specially formed tones can be made to sound as if the sequence continues ascending or descending forever.
|
Before moving on to examine the movement of pitch standards over time it might be instructive to consider an alternative look at pitch. This extract is taken from Music and Your Health - The Relevance of Concert Pitch by Patrick Thilmany which is to be found on the ANAWME (The Association of North American Waldorf Music Educators) web site.
|
The earliest conventions of Western music held that "Music on earth was a reflection of the greater 'music of the spheres', a harmony created by relative distances and rates of motions of the planets - a harmony that was constantly present, if only people were sufficiently sensitive to hear it" (Yudkin, Jeremy, Music in Medieval Europe, 1989). If we as individuals can identify with the concepts presented in this statement, and we accept that we as human beings are multifaceted creatures who must live in harmony with our environment in order to maintain our health and reach our full potential, we can begin to see into the secrets of music and its impact on our health. Such a philosophy would indicate that music should be based in nature and the cosmic rhythms of the universe, if it is to be beneficial to humanity. From this standpoint one can extrapolate that the standard used to determine concert pitch should have an organic foundation as well. One theory of setting the standard for a concert A at 432 Hz attempts to utilize the argument that 432 Hz is based in nature. This theory would indicate by deduction that 440 Hz would then lend itself to generating an unhealthy effect in the environment. To be sure, this debate becomes a very heady and esoteric conversation. Some of the more radical proponents of 432 Hz as the true basis for concert pitch would indicate that everything in nature has a basis in 432 vibrations per second, most of which has not been verified and/or is not verifiable. There is one realm of nature that does support the idea that 432 Hz has an organic basis - that is the movement of the sun. Without going into a lengthy technical monologue we can ascertain that the note C of a scale based on 432 Hz can be reduced to a vibration rate of one vibration per second. We can further establish that the true origination for the measure of one second is based on the movement of the sun. There are further, more in depth, studies based on planetary motion and the harmonic overtones and undertones which do lend further support to the "organic" basis of 432 Hz as a solid foundation for musical structure. The tuning of a scale based on 440 Hz does not lend itself to a reduction on any basis which corresponds to a cosmic movement or rhythm. The difference between 440 Hz and 432 Hz is only 8 vibrations per second, but it is a perceptible difference in the human experience.
|
The Schiller Institute, for example, has been in the forefront of attempts to 'return' pitch to a' = 432 Hz, which was chosen as the pitch standard for Italy at a musical congress that took place during the June 1881 Milan Musical Exposition. We quote a relevant passage from their web site.
|
The Schiller Institute has become known internationally for its initiative to lower the international standard musical pitch to C = 256 Hz (A = 432 Hz.), in order to preserve the human voice and return the performance of Classical music to the pitch for which it was written. The Institute's 1992 publication of A Manual on the Rudiments of Tuning and Registration, Vol. I, Introduction and Human Singing Voice, is creating an educated leadership in the music world to return the pitch to that for which all the great Classical music was written - known as the "Verdi pitch" - and to save the human voice. No less than a revolution in musical history was unleashed on April 9, 1988 in Milan, Italy, when the Schiller Institute brought together some of the world's most highly regarded Classical singers and instrumentalists, to demand a return to rationality in musical tuning and performance. At a conference held at the Casa Giuseppe Verdi, conference speakers, including Lyndon H. LaRouche, Jr., who had conceived the initiative, called for an end to the high-pitched tuning, which has been literally destroying all but the most gifted voices during the past century, and for a return to the principles of Classical aesthetics, according to which the process of musical composition is just as lawful as are the orbits of the planets in the solar system. To underline this call, the conference resolved to introduce legislation into the Italian parliament which would require a return to the natural tuning at which middle-C equals precisely 256 cycles per second - significantly lower than the current tuning which sets A at 440 cps, or frequently even higher |
What one should make of these two extracts, the author leaves to his reader, but it is worth pointing out that while the belief that Verdi espoused the pitch a'=432 Hz. is supported by a letter from Verdi to his librettist, Arrigo Boito, that advocated a lower pitch for colouristic reasons, it is not at all clear that Verdi's suggestion had any philosophical basis at all.
|
|
|
History of Musical Pitch
::

|
Key word:
history of pitch |
| 1 |
'History of Musical Pitch' - a table prepared by Mr. A. J. Ellis and published in 1880 (with additions from later publications)
| units, hertz or Hz, are equivalent to vibrations per second
c'' (one octave above middle C, C5 in scientific notation) is calculated from a' (A4 in scientific notation) using equal temperament
c' (middle C, C4 in scientific notation) is calculated from a' (A4 in scientific notation) using equal temperament
if another note was originally measured this has been converted to a' using equal temperamentall pitches assume an ambient temperature of 59° Fahrenheit (15° centigrade)The speed of sound in air increases as the square-root of temperature
The speed of sound in air at 0° centigrade is 331.5 m/s, and it increases by 0.6 m/s for each increase of 1° centigrade |
a' (A4, la3)
(in hertz) |
c'' (C5, do4)
(in hertz) |
c' (C4, do3)
(in hertz) |
Place | Date | Description |
| 376.3 | 447.5 | 223.75 | Lille, France | 1700 (anté) | Pitch taken by Delezenne from an old dilapidated organ of l'Hospice Comtesse |
| 378.8 | 450.5 | 225.25 | Paris, France | 1766 | Pitch calculated from data given by Dom Bédos in L'Art du Facteur d'Orgues |
| 380.0 | 451.9 | 225.95 | Heidelberg, Germany | 1511 | Pitch calculated from data given by Arnold Schlick |
| 392.2 | 469.1 | 234.55 | St. Petersburg, Russia | 1739 | Euler's clavichord |
| 395.8 | 470.7 | 235.35 | Versailles, France | 1789 | Organ of the palace chapel |
| 398.0 | 473.3 | 236.65 | Berlin, Germany | 1775 | Pitch estimated from a flute described by Jean Henri Lambert in Observations sur les Flûtes, pub. Académie Royal des Sciences, Berlin |
| 400.0 | 475.7 | 237.85 | Paris, France | c. 1756 | Pitch estimated from a flute made by T Lot, one of the five 'maîtres constructeurs' of wind-instruments in Paris, France |
| 401.3 | 477.8 | 238.9 | Paris, France | 1648 | Mersenne's Spinet |
| 404.0 | 480.4 | 240.2 | Paris, France | 1699 | Paris Opera A |
| 405.8 | 482.6 | 241.3 | Paris, France | 1713 | Sauveur's calculation |
| 407.9 | 485.0 | 242.5 | Hamburg, Germany | 1762 | Organ of St. Michael's Church, Hamburg |
| 408-409 | n/a | n/a | Italy | seventeenth century | tuono corista |
| 409.0 | 486.4 | 243.2 | Paris, France | 1783 | Tuning fork of Pascal Taskin, court tuner |
| 415.5 | 494.1 | 247.05 | Dresden, Germany | 1722 | Organ of St. Sophia |
| 419.6 | 499.0 | 249.5 | Seville, Spain | 1785 & 1790 | Organ of Seville cathedral |
| 421.6 | 501.3 | 250.65 | Vienna, Austria | 1780 | supposed to be Mozart's pitch |
| 422.5 | 502.4 | 251.2 | London, England | 1751 | Handel's tuning fork |
| 423.5 | 503.6 | 251.8 | London, England | 1711 | an existing tuning fork of John Shore | | 425.5 | 506.0 | 253.0 | Paris, France | 1829 | Pianoforte at the Paris Opera | | 427.6 | 508.5 | 254.25 | Paris, France | 1823 | Opèra Comique | | 430.8 | 512.3 | 256.15 | Paris, France | 1830 | Opera pitch as related by Drouet, the celebrated French flautist |
| 432.0 | 513.7 | 256.85 | Brussels, Belgium | 1876 | Proposed pitch standard |
| Milan, Italy | 1881 | at a musical congress in Milan as part of the Musical Exposition held in June 1881, it was decided to stabilise pitch in Italy at a'=432.
[quoted in a message on http://launch.groups.yahoo.com/group/earlyflute/message/8074] |
| 432.54 | 512.00 | 256.00 | Paris, France | c.1700 | 'Joseph Sauveur's Philosophical Pitch, C-512', also called 'scientific pitch', fixed middle C at exactly 256 Hz (arrived at by computing the ninth power of 2) and resulted in the A above it (a') being tuned to approximately 430.54 Hz. It gained some popularity due to its mathematical convenience (the frequencies of all the Cs being a power of two) but it never received the same official recognition as diapason normal (a'=435 Hz) and was not as widely used. Joseph Sauveur (1653-1716) was a French physicist and mathematician |
| 433.0 | 512.54 | 256.27 | London, England | 1820 | Ellis reported, at a meeting of the Musical Association held on 4 Apr. 1881, that this pitch was introduced in England by Sir George Smart - indeed it was known as Smart's pitch in England for a long time before the 'Diapason Normal' was constructed. Ellis' appendix in Helmholtz's On the Sensations of Tone as a Physiological Basis for the Theory of Music reports that the pitch was adopted 'with much hesitation' for the London Philharmonic Society in about 1820 |
| 435.0 | 517.3 | 258.65 | Paris, France | 1859 | The French 'Diapason Normal', set in a law passed on 16 February
1859 by the French government acting with the advice of Halvy, Meyerbeer, Auber, Ambroise Thomas and Rossini, although the mean of several forks set to this pitch lies slightly higher at a'=435.4 which is equivalent to c''=517.8 or c' = 258.9. This pitch was adopted outside France. For example, several Italian institutions, including the Istituto Musicale di Firenze (Florence) and the Teatro San Carlo in Naples adopted the French 'Diapason Normal' |
| 437.0 | 519.7 | 258.85 | Paris and Toulouse, France | 1836 & 1859 | The earlier was the pitch of the Italian Opera in Paris, the later that of the Conservatoire in Toulouse |
| 440.0 | 523.25 | 261.625 | Paris, France | 1829 | Orchestral pitch of the Paris Opera | | 440.0 | 523.25 | 261.625 | Stuttgart, Germany | 1838 | Proposed pitch standard, Stuttgart congress (actually a'=440.2 when corrected to table temperature); also Scheibler's standard. |
| 440-443 | n/a | n/a | Italy | 17th century | tutto punto |
| 441.0 | 524.4 | 262.2 | Rome, Italy | 1725 (anté) | Pitch calculated from a flute made by Biglioni and possibly brought from Rome by J. J. Quantz when he left Rome in 1725 |
| 444.0 | 528.0 | 264.0 | London, England | 1860 | Standard intended for the Society of Arts - (however a fork set to this standard by J.H. Griesbach has a measured pitch of a'=445.7, equivalent to c''=530.1 or c'=265.05) |
| 444.5 | 528.6 | 264.3 | Madrid, Spain | 1858 | Theatre Royale, Madrid |
| 444.5 | 528.6 | 264.3 | London, England | c. 1810 | Pitch of a flute made by Henry Potter |
| 444.6 | 528.7 | 264.35 | London, England | 1877 | Organ in St. Paul's Cathedral |
| 444.8 | 528.9 | 262.45 | Turin, Weimer, Würtemberg | 1859 | Measurements made for the French Commission |
| 445.7 | 530.1 | 265.05 | London, England | 1860 | see comment for a'=444.0 (above) |
| 446.0 | 530.4 | 265.2 | Paris, France; Dresden and Pesth, Germany, | 1859 | Pleyel's Piano taken by Delezenne and the pitches at the Opera houses of Dresden and Pesth |
| 447.11 | 531.7 | 265.85 | London, England | 1845 | Pitch calculated from a fork said to be at the pitch of the Royal Philharmonic Society |
| 448.0 | 532.8 | 266.4 | Hamburg, Germany | 1839 & 1840 | Opera | | 448.0 | 532.8 | 266.4 | Paris, France | 1854 | Opéra Comique | | 448.0 | 532.8 | 266.4 | Paris, France | 1858 | Grand Opèra | | 448.0 | 532.8 | 266.4 | Liège, Belgium | 1859 | Conservatoire |
| 450.0 | 535.1 | 267.55 | London, England | 1850 to 1885 | An average of the pitches of London orchestras during this period |
| mid-nineteenth century | Rome, Italy | Accademia di Santa Cecilia in Rome adopted as its own pitch a'=450. Other musical institutions adopted the French 'Diapason Normal' while others used a'=432 |
| 450.5 | 535.7 | 267.85 | Lille, France | 1848 & 1854 | Lille Opera, measured during performance | | 451.0 | 536.3 | 268.15 | Brussels, Belgium | 1879 | Pitch standard proposed for the Belgian Army | | 451.5 | 536.9 | 268.45 | St. Petersburg, Russia | 1858 | Opera | | 451.7 | 537.2 | 268.6 | Milan, Italy | 1867 | La Scala Opera | | 451.8 | 537.3 | 268.65 | Berlin, Germany | 1859 | Opera |
| 451.9 | 537.4 | 268.7 | London, England | 1878 | British Army Regulations |
| 452.0 | 537.5 | 268.75 | Lille, France | 1859 | Conservatoire |
| 452.0 | 537.5 | 268.75 | London, England | 1889 | Official Pitch at the 'Inventions' Exhibition in 1885 - the highest pitch used intentionally by English orchestras up to 1890 |
| 452.5 | 538.2 | 269.1 | London, England | 1846 to 1854 | Mean pitch of the Philharmonic Band under Sir Michael Costa. His Majesty's Rules and Regulations required Army Bands to play at the Philharmonic pitch, and a fork tuned to a'=452.5 in 1890 is preserved as the standard for the Military Training School at Kneller Hall |
| 453.3 | 539.0 | 269.5 | London, England | 1837 (anté) | Pitch calculated from a flute made by Rudall and Rose possibly as early as 1827 |
| 454.08 | 540.0 | 270.0 | London, England | 1874 | Old Philharmonic Pitch, instigated by Sir Charles Hall |
| 454.7 | 540.8 | 270.4 | London, England | 1874 | Fork representing the highest pitch adopted for Philharmonic concerts | | 454.7 | 540.8 | 270.4 | London, England | 1879 | Steinway's English pitch; also Messrs. Bryceson's pitch |
| 455.3 | 541.5 | 270.75 | London, England | 1879 | Messrs. Erard's pitch | | 455.5 | 541.7 | 270.85 | Brussels, Belgium | 1859 | Band of the Guides | | 456.1 | 542.4 | 271.2 | London, England | 1857 | Fork set to the French Society of Pianoforte Makers | | 457.2 | 543.7 | 271.85 | New York, USA | 1879 | Pitch used by Messrs. Steinway in America |
| 456.0 | 542.30 | 271.15 | Vienna, Austria | 1859 | Viennese 'high pitch' |
| 457.6 | 544.2 | 272.1 | Vienna, Austria | c. 1640 | Great Franciscan organ |
| 460.0 | 547.05 | 273.525 | Vienna, Austria | 1880 | Old Austrian Military Pitch |
| 460-470 | n/a | n/a | Italy | seventeenth century | mezzo punto |
| 460.8 | 548.0 | 274.0 | America | 1875 | the pitch to which a number of American institutions worked, as reported by Ellis in his appendix to Helmholtz's On the Sensations of Tone as a Physiological Basis for the Theory of Music |
| 461.0 | 548.3 | 274.15 | London, England | 1838 (anté) | Actual pitch of a flute said to be tuned to a'=453.3 |
| 474.1 | 563.8 | 281.9 | Durham, England | 1683 | Cathedral Organ by Bernhardt Smith | | 474.1 | 563.8 | 281.9 | London, England | 1708 | Organ of the Chapel Royal by Bernhardt Smith | | 480.8 | 571.8 | 285.9 | Hamburg, Germany | 1543 & 1879 | Organ at the church of St. Catherine | | 484.1 | 575.7 | 287.85 | Lübeck, Germany | 1878 | Cathedral, small organ | | 489.2 | 581.8 | 290.9 | Hamburg, Germany | 1688 & 1693 | Organ at the church of St. Jacob | | 505.6 | 601.4 | 300.7 | Paris, France | 1636 | Mersenne's church pitch |
| 506.9 | 602.9 | 301.45 | Halberstadt, Germany | 1361 | Cathedral Organ |
| 567.6 | 675.2 | 337.6 | Paris, France | 1636 | Mersenne's chamber pitch |
| 570.7 | 678.7 | 338.35 | Germany | 1619 | Pitch called Kammerton (chamber pitch) by Praetorius; also called North German church pitch |
Gill Green's History of Piano Tuning tells us that pitch varied from town to town in England as well, providing another tuning headache: in 1880 Henry Fowler Broadwood wrote to George Rose regarding the difficulty of supplying instruments for provincial tours:
|
I will not send out new non-concert instruments, therefore the regular concert instruments form our only resource - then again I will not send these packed - but only in a van - and accompanied by a tuner. |
A letter to The Pianomaker in 1913 showed the extent to which the problem had escalated: despite an agreement being made in the 1890s to standardize pitch, military bands were a law unto themselves, fuelled by cynical instrument makers in league with bandmasters who changed pitches arbitrarily to force bandsmen to periodically renew their instruments. T.G. Dyson, then the President of the Music Trades Association of Great Britain, wrote:
|
So long as the military bands retain their present pitch (C=537.5 Hz), it must be recognized; but there is no reason why some eight other pitches should not be swept out of the way for musical purposes, leaving the international pitch (C=517.3 Hz) which is now the only recognized pitch in America as well as on the Continent, and the military band pitch as the low and high pitch of this country. |
Considering the 'international pitch' had been in effect for over twenty years at that time, it seemed to have had little or no effect on the music world in general, if Dyson was referring to 'some eight other pitches'.
In 1896 A.J. Hipkins wrote in his History of the Pianoforte that:
|
The French pitch, or Diapason Normal, is now generally adopted on the Continent and has made its way to the United States of America. In this country, with the exception of the Italian opera, which has been at the low pitch for the last 15 years, we may say the high or Philharmonic pitch has, from 1846 to 1895, prevailed. ... The Philharmonic Society, has, however, for 1896, relinquished its high pitch and adopted the Diapason Normal. |
Different piano makers had their own pitches: from 1849-1854 Broadwoods used A=445.9 Hz, escalating to A=454.7 Hz in 1874. Collard's 1877 pitch was A=449.9 Hz, Steinway (in England) in 1879 used A=454.7 Hz, Erard used A=455.3 Hz and in 1877 Chappell tuned at to 455.9 Hz.
No wonder that in June 1860 The Society of Arts established a commission to try to establish a single UNIFORM MUSICAL PITCH.
| pitches in use in England in the 1920s : frequencies in Hz : taken from Notes on Concertina Pitch |
| note | Normal (-20 cents to ISO) | New Philharmonic (-4 cents to ISO) | Stuttgart/ISO | Society of Arts (+22 cents to ISO) | Old Philharmonic (+54 cents to ISO) |
| A | 434.91 | 438.95 | 440 | 445.68 | 454.08 |
| A# | 460.77 | 465.05 | 466.16 | 472.18 | 481.09 |
| B | 488.17 | 492.70 | 493.88 | 500.25 | 509.69 |
| C | 517.20 | 522.00 | 523.25 | 530.00 | 540.00 |
| C# | 547.95 | 553.04 | 554.37 | 561.52 | 572.11 |
| D | 580.54 | 585.93 | 587.33 | 594.90 | 606.13 |
| D# | 615.06 | 620.77 | 622.25 | 630.28 | 642.17 |
| E | 651.63 | 657.68 | 659.26 | 667.76 | 680.36 |
| F | 690.38 | 696.79 | 698.46 | 707.47 | 720.81 |
| F# | 731.43 | 738.22 | 739.99 | 749.53 | 763.68 |
| G | 774.92 | 782.12 | 783.99 | 794.10 | 809.09 |
| G# | 821.00 | 828.62 | 830.61 | 841.32 | 857.20 |
| A | 869.82 | 877.90 | 880.00 | 891.35 | 908.17 |
| A# | 921.55 | 930.10 | 932.33 | 944.35 | 962.17 |
| B | 976.34 | 985.40 | 987.77 | 1000.51 | 1019.38 |
| C | 1034.40 | 1044.00 | 1046.50 | 1060.00 | 1080.00 |
References:
History of Piano Tuning
The Rise and Fall of English Pitch
Society of Arts Pitch: Part I - A Meeting is convened
Society of Arts Pitch: Part II - Report of the Committee
Society of Arts Pitch: Part III - Discussion and Action Arising
Edward Solomon, writing in The Trombone Forum, notes, about the drop in pitch of brass instruments, that in the UK at least, military bands all changed to low pitch in 1928. The brass band movement, however, didn't embrace low pitch until 1966. Solomon don't think military bands ever had much influence over brass bands, except perhaps in the very early days during the nineteenth century. The two never really engaged with one another in any formal manner, which is evinced by the brass band movement's stubborn insistence on maintaining their own high pitch long after both military bands and orchestras had changed to low pitch in Britain.
|
|
|
Harmonic or Overtone Series
::

|
Key words:
harmonics
fundamental
overtones |
| 1 |
Harmonic or Overtone Series
Sauveur, following on from work, published in 1673, by two Oxford men, William Noble and Thomas Pigot, noted that a vibrating string produces sounds corresponding to several of its harmonics at the same time. The dynamical explanation for this was first published in 1755 by Daniel Bernouilli (1700-1782). He described how a vibrating string can sustain a multitude of simple harmonic oscillations. We call this the 'superposition principle'. The harmonics are integer multiples of the 'fundamental frequency', also called the 'first harmonic' or 'generator'. So for a string with a fundamental frequency of 440 Hz, that is fixed at both ends, the harmonics are integral multiples of 440 Hz; i.e. 440 Hz (1 times 440 Hz), 880 Hz (2 times 440 Hz), 1320 Hz (3 times 440 Hz), 1760 Hz (4 times 440 Hz) and so on. The term overtone is reserved for those harmonics that lie above the 'fundamental frequency' (also called the 'fundamental' or 'generator').
To see the harmonics of a violin string visit Standing Waves, Medium Fixed At Both Ends which demonstrates visually the 1st, 2nd, 3rd, 4th and 5th harmonics produced by a string on a violin.
The first 15 harmonics (or fundamental plus 14 overtones) are given below, their frequencies set out in the third column. The fourth column, headed 'normalized', is the result of dividing the frequency of the harmonic by powers of 2 (transposing the sound down one octave for each power of 2) so that it lies within a single octave (between 440 Hz and 880 Hz). The nearest note in the chromatic scale on A is given in the fifth column while the last column, headed %, shows how close the normalized frequency is to the frequency of the nearest equal-tempered note diatonic to A.
| harmonic | overtone | frequency | normalized | note name (in ET) | closeness in % to note (in ET)
expressed as a ratio of frequencies:
100%, very close or exact
less than 100%, harmonic is flat
greater than 100%, harmonic is sharp |
| 1 | Fundamental | 440 Hz | 440 Hz | A | 100% | 0 cents (exact) |
| 2 | 1 | 880 Hz | 440 Hz | A | 100% | 0 cents (exact) |
| 3 | 2 | 1320 Hz | 660 Hz | E | 100.1% | 1.96 cents sharp |
| 4 | 3 | 1760 Hz | 440 Hz | A | 100% | 0 cents (exact) |
| 5 | 4 | 2200 Hz | 550 Hz | C# | 99.2% | 13.69 cents flat |
| 6 | 5 | 2640 Hz | 660 Hz | E | 100.1% | 1.96 cents sharp |
| 7 | 6 | 3080 Hz | 770 Hz | G | 98.2% | 31.17 cents flat |
| 8 | 7 | 3520 Hz | 440 Hz | A | 100% | 0 cents (exact) |
| 9 | 8 | 3960 Hz | 495 Hz | B | 100.2% | 3.91 cents sharp |
| 10 | 9 | 4400 Hz | 550 Hz | C# | 99.2% | 13.69 cents flat |
| 11 | 10 | 4840 Hz | 605 Hz | D or D#
D# slightly closer | D 103%
D# 97.2% | 51.32 cents sharp
48.68 cents flat |
| 12 | 11 | 5280 Hz | 660 Hz | E | 100% | 1.96 cents sharp |
| 13 | 12 | 5720 Hz | 715 Hz | F or F#
F slightly closer | F 102.4%
F# 97.6% | 40.53 cents sharp
59.47 cents flat |
| 14 | 13 | 6160 Hz | 770 Hz | G | 98.2% | 31.17 cents flat |
| 15 | 14 | 6600 Hz | 825 Hz | G# | 99.3% | 11.73 cents flat |
| * The cent is a logarithmic measure of a musical interval invented by Alexander Ellis. It first appears in the appendix he added to his translation of Herman von Helmholtz's 'On the Sensation of Tone As a Physiological Basis for the Theory of Music' [in German, 1863; Ellis's English translation with Appendix, 1875]. A cent is the logarithmic division of the equitempered semitone into 100 equal parts. It is therefore the 1200th root of 2, a ratio approximately equal to (1:1.0005777895) The formula for calculating the 'cents-value' of any interval ratio is: cents = log10(ratio) * [1200 / log10(2)] or
cents = 1200 × log2 (ratio)
Intervals expressed in cents are added while those expressed in ratio form must be multiplied: for example, a perfect fourth plus a perfect fifth equals an octave. In ratio form, (4:3) times (3:2) = (12:6) = (2:1), in cents, 498.045 + 701.955 = 1200
We have provided an online calculator that converts frequency ratios to cents |
If you wish to investigate higher harmonics please refer to our interval calculator.
We can extract a complete diatonic scale on A from the first 15 harmonics. The D is somewhat sharp while the F#, in particular, is very flat. It would not be impractical to tune a stringed instrument to play diatonic melodies in the key of A using this scale. You will see that the perfect fifth appears in this harmonic series as the third harmonic. The ratio of the frequencies of the third and second harmonic is (1320:880) which is (3:2). However the fourth, the note D, which should have a frequency in ratio to A of (4:3) (1.33333), actually comes out as 1.375. A more serious problem is the absence of an interval one could call a tone or a semitone. The Greeks defined their tone as the difference between a perfect fifth and a perfect fourth, but the fourth is not perfect in this scale. There is no way of deriving chromatic scales either by starting from A or by starting from another note, say, the perfect fifth, E.
We notate below the harmonic or overtone series based on C. The overtones shown in brackets are only approximately equivalent to the equal tempered scale notes on the staff. The overtone count (1, 2, 3, etc.) are one more than the harmonic count in the table above (1, 2, 3, etc.). So the first overtone is the second harmonic. Some commentators call the fundamental (or first harmonic) the 'zeroth' overtone.

|
|
|
Inharmonicity
::

|
Key words:
inharmonicity
harmonic overtones
inharmonic overtones |
| 1 |
Inharmonicity
Before leaving the discussion of harmonics, it would be useful to point out that not all systems produce their harmonics as neatly as, say, the strings of a violin. Some instruments produce harmonics that are not integer multiples of the fundamental. The term inharmonicity is used in music for the degree to which the frequencies of the overtones of a fundamental differ from whole number multiples of the fundamental's frequency. These inharmonic overtones are often distinguished from harmonic overtones, which are all whole number multiples, by calling them partials, though partial may also be used to refer to both. Since the harmonics contribute to the sense of sounds as pitched or unpitched, the more inharmonic the content of a sound the less definite it becomes in pitch. Many percussion instruments such as cymbals, tam-tams, and chimes, create complex and inharmonic sounds. However, strings too, become more inharmonic the shorter and thicker they are, which is an important consideration for piano tuners, especially when setting the thick strings of the bass register. Strings on a piano are generally thicker and therefore shorter than those on harpsichords in order, as we learn from the harpsichord and piano maker Johann Andreas Stein writing in 1769, to accommodate "the blow of the hammer."
Inharmonicity is found, also, in the instruments of the gamelan, particularly in the overtones of the free vibrations of the gongs, bells and strings. The inharmonic partials of the instruments require that the octave be stretched by a ratio of 2.02/1, or 17 cents (100ths of a semitone in 12-tone equal temperament) per octave. The stretched octave sounds more harmonious when tuned so frequencies of vibration coincide, rather than when tuned exactly.
Galembo and Cuddy, in their paper to the 134th meeting of the Acoustical Society of America entitled Large grand vs. small upright pianos: factors of timbral difference, write that:
|
Schuck and Young in 1943 were the first to measure the spectral inharmonicity in piano tones. They found that the spectral partials in piano tones are progressively stretched and hypothesized that the lower inharmonicity of longer strings in the bass range explains why musicians prefer grand piano tone quality over that of uprights.
Nineteen years later, Harvey Fletcher with collaborators found that the spectral inharmonicity is important for tones to sound piano-like. They proposed that inharmonicity is responsible for the "warmth" property common to real piano tones.
Fletcher et al.'s statement about the importance of inharmonicity for timbre provided a perceptual basis to the hypothesis of Shuck and Young. Since then, experts have commonly attributed the primary difference in the quality of bass tones in small vs. large pianos to the difference in the inharmonicity between short and long strings. The influences of other acoustical or design factors have never been given serious experimental consideration.
|
It should also be remembered that, so far as the piano is concerned, it is the sound board that radiates the energy from a vibrating string, and not the string itself, so the natural resonances of the sound board also play a part in determining the tone we hear. This is explained more fully in the reference below.
References:
|
|
|
Pythagorean Series
::

|
Key words:
tuning
temperament
Pythagoras |
| 1 |
Pythagorean Series
Before going any further we should clarify the distinction between tuning and temperament. We quote below from Pierre Lewis's article Understanding Temperaments.
A tuning is laid out with nothing but pure intervals, leaving the Pythagorean or ditonic comma to fall as it must.
A temperament involves deliberately mistuning some intervals to obtain a distribution of the comma that will lead to a more useful result in a given context. Solutions can be grouped into three main classes:
- tunings (Pythagorean, just intonation)
- regular temperaments where all fifths but the wolf fifth are tempered the same way; note: regular meantone implies that all major thirds are identical
- irregular temperaments where the quality of the fifths around the circle changes, generally so as to make the more common keys more consonant
Temperaments are further classified as:
- circulating or closed if they allow unlimited modulation, i.e. enharmonics are usable (equal temperament, most irregular temperaments)
- non-circulating or open otherwise (tunings, most regular temperaments)
The choice of a particular solution depends on many factors such as
- the needs of the music (harmonic vs melodic, modulations)
- the tastes of the musicians and listeners
- the instrument to be tuned (organ vs harpsichord - tuning the former is much more work so one needs a more convenient solution),
- aesthetic (Gothic's tense thirds and pure fifths vs the stable, pure thirds of the Renaissance and Baroque) and theoretical considerations, and
ease of tuning (equal temperament is one of the more difficult)
|
We should first ask whether the perfect fifth, one of the three intervals (octave, fifth, and fourth) which have been considered to be consonant throughout history by essentially all cultures, form a logical base for building a chromatic scale; for example, one starting from the note C?
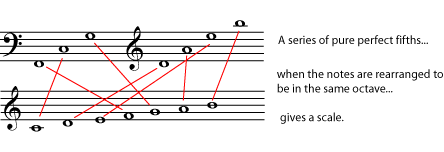
We illustrate above a sequence of fifths starting from F, two octaves below middle C. The image is taken from Tuning Systems by Catherine Schmidt-Jones.
A sequence starting from C would progress as follows: C G D A E B F# C# G# D# A# F C, the first 7 members providing us with the diatonic scale of G major (G A B C D E F# G) If one applies the ratio (3:2) twelve times, and normalizes the result by dividing by powers of 2, the result is sharp of an octave by a ratio called the Pythagorean or ditonic comma (524288:531441). We find also that if we use these frequencies to construct a scale, the major third (G B) and the octave (G G, the latter generated from the twelfth power of (3/2)) are both too large.
| Pythagorean intervals and their derivations (also called by modern theorists, the 3-limit system because all ratios are powers only of 2 and/or 3)
| | Interval | Ratio | Derivation | Cents |
| Unison | (1:1) | Unison 1:1 | 0.000 |
| Minor Second | (256:243) | Octave - Major Seventh | 90.225 |
| Major Second | (9:8) | (3:2)2 | 203.910 |
| Minor Third | (32:27) | Octave - Major Third | 294.135 |
| Major Third | (81:64) | (3:2)4 | 407.820 |
| Fourth | (4:3) | Octave - Fifth | 498.045 |
| Augmented Fourth | (729:512) | (3:2)6 | 611.730 |
| Fifth | (3:2) | (3:2)1 | 701.955 |
| Minor Sixth | (128:81) | Octave - Major Third | 792.180 |
| Major Sixth | (27:16) | (3:2)3 | 905.865 |
| Minor Seventh | (16:9) | Octave - Major Second | 996.090 |
| Major Seventh | (243:128) | (3:2)5 | 1109.775 |
| Octave | (2:1) | Octave (2:1) | 1200.000 |
A number of proposals have been considered in order to 'improve' the Pythagorean scale.
For instance, the Greek major tone, represented by the ratio (9:8) could be married to the semitone, represented by the ratio (256:243) and a scale of five whole tones plus two semitones could be formed. Now the octave is exact but the thirds are still sharp and, because the sharps and flats are not enharmonic, there are problems when changing key. Another solution employed a pure fourth (4:3) and set the octave as a pure fourth above a perfect fifth, before using the ratio (9:8) to fill in the remaining tones. The remaining semitones were chosen on the basis of taste. Unfortunately, the third is still sharp! A further solution was to slightly narrow the fifth in every or in only some of the notes arising from the circle of fifths, so absorbing the comma of Pythagoras. This kind of solution made it possible to move from one key to any other and formed the basis of the well-tempered system promoted in 1722 and again in 1724 when Bach published his "Well-Tempered Clavier". The series of keyboard preludes and fugues was written as much to show the characteristic colour of different keys as to demonstrate that, using this tuning system, a composer was no longer prevented from exploring every minor and major key.
|
|
|
Meantone Scale
::

|
Key word:
meantone scale |
| 1 |
Meantone Scale
The first mention of temperament is found in 1496 in the treatise Practica musica by the Italian theorist Franchino Gafori, who stated that organists flatten fifths by a small, indefinite amount. This practice was formalised in what is called the mesotonic or meantone (also written mean-tone) scale. It was always particularly favoured by organists and explains why organ music from the period the early sixteenth to the nineteenth century was written in a relatively small number of keys, those that this scale favoured. Arnolt Schlick's Spiegel der Orgelmacher und Organisten (1511) described both the practice of and formulae for mean-tone tuning which makes it clear that it was already in use. Pietro Aron produced a more thorough analysis in Toscanello in Musica (1523), which sufficed for all practical purposes. The earliest complete description was published by Francisco de Salinas in De Musica libri septem (1577). How was it set? Based on C, the method relied on using the first five notes from the circle of fifths from C, namely C, G, D, A, E and setting a pure third between C-E by narrowing the fifths by a small amount - from a ratio of (3:2) to a ratio of (2.99:2). D, the note between C and E was set so that the ratio between D and C was identical to that between E and D, so placing D in the mean position between C and E, hence the scale's name. What happened after this to complete the chromatic scale introduced a number of variants which only the more studious of our readers are likely to pursue. Suffice it to point out that the results generally work well in the keys C, G, D, F and B flat but outside these serious problems arise and composers writing for this system avoided keys more distant from C. Pietro Aron's description of meantone tuning is the best known. All but one of the fifths are flattened from the pure (3:2) ratio by 1/4 of the syntonic comma. The remaining fifth ends up being sharp by 1 3/4 of the syntonic comma (the wolf). The syntonic comma is the ratio (9:8) divided by (10:9), which is the ratio between a pure C-D interval and a pure D-E interval. In a pure harmonic series starting at CCC (CCC is English organ nomenclature: bottom C on a 16' voice), middle C is 8 times the fundamental, middle D is 9 times the fundamental, and middle E is 10 times the fundamental. The result of this procedure is a scale with 8 pure major 3rds and 4 diminished 4ths. But there were other meantone procedures known in the 16th and 17th centuries, especially by 2/7th comma, in which the minor 3rds are pure and the major 3rds beat, and 1/3rd comma. In the the mid-eighteenth century, several instrument-makers and theoreticians used a 1/6th comma meantone temperament, particularly Gottfried Silbermann and Vallotti. A bizarre fact is that equal temperament is really meantone by 1/12th comma, that is every fifth is narrowed by 1/12 of the syntonic comma and the interval between C - D and between D - E are equal. So, all the modern pianos you have ever heard are in one of the many types of meantone temperament!
|
|
|
Equal Temperament
::

|
Key word:
equal temperament |
| 1 |
Equal Temperament
It must have been a brave man who first pointed out to a world wedded to centuries of mean, natural and Pythagorean tuning, that a scale could be formed using a universal ratio for a semitone such that successive application of this ratio generated the notes of a chromatic scale before completing the octave with its harmonic ratio of (2:1), and that using such a system one might play in tune in any key. This universal ratio is the twelfth root of 2. This tuning system, called 12EDO (Equal Divisions of the Octave), 12-tET by modern tuning theorists or Standard European 1/12 Diatonic Comma Equal Temperament by others, found favour amongst the lutenists of the sixteenth century who, having tuned the instrument's strings to different notes, could fret each at an identical point from the nut to produce parallel equal-tempered scales something that would be impossible using any other temperament. Unfortunately, as Nicola Vicentino, the inventor of the archicembalo with six rows of keys that enabled six different versions of any scale to be performed complete with temperamental adjustment, observed, this produced horrible clashes between the lute tuned to an equal-tempered scale performed with a keyboard tuned using mean-tone temperament.
Evidence of the use of equal temperament in consort singing comes in the madrigal O voi che sospirate a miglior note by Luca Marenzio (c.1553-1599). The composer modulates completely around the circle of fifths within a single phrase, using enharmonic spellings within single chords (for instance, simultaneous C# and Db), which would be impossible to sing unless some approximation of equal temperament is being observed.
At the time, keyboard players found the equal-tempered scale more 'sour' than the other systems in the five keys commonly used, and because most composers worked only in a limited number of keys the benefits to be had from the equal-tempered system in more distant keys were not at all obvious. This probably helped delay its acceptance until such time as enough 'new' ears had become used to it, or enough composers had explored more distant keys with it in mind. In England, it was not until 1842 that the first organ, that of St. Nicholas in Newcastle-upon-Tyne, was tuned to equal temperament. It is still surprising that the system may have been known in Europe as early as the fifteenth century (some have suggested that equal temperament was first explained by Chu Tsai-yü in a paper entitled A New Account of the Science of the Pitch Pipes published in 1584). However, Henricus Grammateus had already drawn up a fairly close approximation in 1518, and Zarlino corrected Vincenzo Galilei's plan for a twelve-stringed equal-tempered lute (Galilei had invoked Aristoxenus as his inspiration in this project). Even though the mathematician and music theorist Mersenne produced a correct and systematic description in 1635, equal temperament was not adopted until 150 years later in Germany and Austria, while Britain and France delayed for over two centuries. As late as 1879, William Pole was writing in his book The Philosophy of Music, "The modern practice of tuning all organs to equal temperament has been a fearful detriment to their quality of tone. Under the old tuning, an organ made harmonious and attractive music. Now, the harsh 3rds give it a cacophonous and repulsive effect." In 1940, another sceptic, L. S. Lloyd, wrote an article entitled The Myth of equal Temperament in which he described the improbability of singers, or players of any instrument with variable intonation of being able to sing or play in true equal temperament; or, a keyboard instrument actually being tuned to theoretically correct equal temperament. It is worth remembering that Vincenzo Galilei (1520-1591), an Italian lutenist, composer, and music theorist, and the father of the famous astronomer and physicist Galileo, observed that instrumentals and singers failed generally to observed any theoretical tuning or temperament. As Barolsky writes "all intervals, Galilei argued, are natural, not simply those mathematically determined. In performance, a fifth that is a bit off the (3:2) ratio is just as useful as one that is exactly on the mark."
It is interesting to read what the German composer, violinist and conductor Louis Spohr (1784-1859), writing in his Violinschule of 1832, has to say on the subject of equal temperament.
| "By pure intonation is naturally meant that of equal temperament [gleichschwebenden], since in modern music no other exists ... The budding violinist needs to know only this one intonation. ..."
|
The clavichord maker Peter Bavington, writing to the Yahoo clavichord-list, comments:
|
Spohr was the central figure in a school of violinists who advocated playing in strict equal temperament (ET): he was certainly not an ivory-tower theorist. However, not every violin teacher agreed with him.
Violin intonation was the subject of an interesting article by Patrizio Barbieri in Early Music a few years ago ('Violin intonation: a historical survey', Early Music, vol. XIX No. 1 (February 1991)). Barbieri, the author of Acustica, accordatura e temperamento nell'illuminismo veneto: con scritti inediti di Alessandro Barca, Giordano Riccati e altri autori, examined many sources and concluded that there was a distinct change from 'harmonic' to 'Pythagorean-expressive' intonation around 1780-1800. If playing in the 'harmonic' intonation, one's aim is to produce good harmony, particularly with the bass, which might lead one, for example, to play the major third of a common chord lower than one might in ET so as to get a nearer-to-pure third. On the other hand, in the 'Pythagorean-expressive' intonation one would seek to emphasise the melodic tendency of a note: thus one might play the leading note in a common chord on the dominant higher than pure, perhaps as high as a Pythagorean third, because it is tending upwards so as to resolve on the tonic. This in turn would lead to a wide third in the chord, perhaps a dissonant third, but that would be resolved.
Barbieri quotes a lot of evidence for this change, which we might perhaps associate with the transition from late-baroque to classical, and in keyboard instruments from mean-tone and other unequal tunings to the universal acceptance of equal temperament.
Two issues later, incidentally, there was another article, this time by Bruce Haynes, covering some of the same ground.
Reference:
Bruce Haynes: 'Beyond temperament: non-keyboard intonation in the 17th and 18th centuries' in Early Music, vol XIX No. 3 (August 1991)
|
The equal-tempered system cannot be derived from rational relationships because the twelfth root of 2, like the square root of 2, is irrational.
Many commentators state that in an equal-tempered scale the fifths are perfect. In fact, the ET-fifth is slightly narrower and the ET-fourth is slightly wider than their just interval equivalents.
The theoretical equal temperament frequencies for the A=440 Hz tuning pitch are: | tuning pitch: a'=440 Hz | | A | 27.500 Hz | 55.000 Hz | 110.000 Hz | 220.000 Hz | 440.000 Hz | 880.000 Hz | 1760.000 Hz | 3520.000 Hz | | A# | 29.135 Hz | 58.271 Hz | 116.541 Hz | 233.082 Hz | 466.164 Hz | 932.328 Hz | 1864.656 Hz | 3729.312 Hz | | B | 30.868 Hz | 61.735 Hz | 123.471 Hz | 246.942 Hz | 493.883 Hz | 987.766 Hz | 1975.532 Hz | 3951.064 Hz | | C | 32.703 Hz | 65.407 Hz | 130.813 Hz | 261.626 Hz | 523.252 Hz | 1046.504 Hz | 2093.008 Hz | 4186.016 Hz | | C# | 34.648 Hz | 69.296 Hz | 138.592 Hz | 277.183 Hz | 554.366 Hz | 1108.732 Hz | 2217.464 Hz | 4434.928 Hz | | D | 36.708 Hz | 73.416 Hz | 146.833 Hz | 293.665 Hz | 587.330 Hz | 1174.660 Hz | 2349.320 Hz | 4698.640 Hz | | D# | 38.891 Hz | 77.782 Hz | 155.564 Hz | 311.127 Hz | 622.254 Hz | 1244.508 Hz | 2489.016 Hz | 4978.032 Hz | | E | 41.204 Hz | 82.407 Hz | 164.814 Hz | 329.628 Hz | 659.256 Hz | 1318.512 Hz | 2637.024 Hz | 5274.048 Hz | | F | 43.654 Hz | 87.307 Hz | 174.614 Hz | 349.228 Hz | 698.456 Hz | 1396.912 Hz | 2793.824 Hz | 5587.648 Hz | | F# | 46.249 Hz | 92.499 Hz | 184.997 Hz | 369.994 Hz | 739.988 Hz | 1479.976 Hz | 2959.952 Hz | 5919.904 Hz | | G | 48.999 Hz | 97.999 Hz | 195.998 Hz | 391.995 Hz | 783.990 Hz | 1567.980 Hz | 3135.960 Hz | 6271.920 Hz | | G# | 51.913 Hz | 103.826 Hz | 207.653 Hz | 415.305 Hz | 830.610 Hz | 1661.220 Hz | 3322.440 Hz | 6644.880 Hz |
|
|
|
Just Intonation
::

|
Key word:
just intonation |
| 1 |
Just Intonation
Barbour writes, in Tuning and Temperament, "it is significant that the great music theorists ... presented just intonation as the theoretical basis of the scale, but temperament as a necessity". Strict adherence to just intonation could, under certain circumstances, lead to pitch descent by tuning, so-called commatic drift.
Commatic drift is defined by Paul Erlich (and quoted in Joe Monzo's Tonalsoft Encyclopedia of Microtonal Music Theory) as "an immediate change in the pitch of a note, as the note is held or repeated from one harmony into another". He continues, "a drift is an overall pitch change of the entire scale. its effect on the pitch of any note doesn't become evident until an entire "comma pump" chord progression has been traversed. For example, in the classic problem of rendering the I-»vi-»ii-»V-»I progression in strict Just Intonation, one either has a shift (the 2nd scale degree shifts from 10/9 in the ii chord to 9/8 in the V chord) and no drift, or a drift (the final I is lower by 80:81 than the initial I) and no shifts."
However, despite many examples of where, were the intervals defined by Just Intonation strictly to be adhered to, there would be a drift in pitch, musicians actually 'correct the pitch' by tempering various intervals. In fact, it is the pitch of individual notes that vary ever so slightly through chordal progressions, the net effect of which is to hold the overall pitch reasonably constant.
The natural or harmonic scale is being explored again in the twentieth century through the work of Harry Partch, Lou Harrison and others who, with the advantages of modern technology, have sought to explore musical systems that were abandoned more for their practical limitations than for any lack of aesthetic interest. One has only to consider the complexity of a piano built to perform music based on a microtonal system, or remind ourselves of Nicola Vicentino's archicembalo, instruments that have been made and played, to appreciate that the equal-tempered scale brings with it certain advantages.
Following on the ideas of Theodor Adorno, the American composer Ben Johnston believes that music has the power to influence and even control social trends. Johnston believes that an equal tempered tuning system based on irrational intervals contributes to the hectic hyper-activity of modern life. The wildly beating sonorities of equal temperament are thought to resemble (and perhaps foment) the fast-paced, unmeditative current of present-day Western existence. Many just intervals lack the sharp vibrancy of irrational intervals (and higher-order rational intervals) and thus are sometimes felt to convey an affect of stasis and meditative calm. Indeed, cultures whose tuning systems draw heavily on purely tuned intervals (e.g., North Indian classical music) tend to value meditative social attitudes more greatly than in the West.
Reference:
Ben Johnston
An interesting 31-note equal temperament, 31EDO (Equal Divisions of the Octave), produces a scale that is much closer to just intonation than the 12-note equal temperament (12EDO) discussed in the previous section. The thirds, (2(8/31) = 1.1958733 and 2(10/31) = 1.2505655), are much nearer just intonation than those of 12-note equal temperament, although the perfect fourth and fifth are less good than 12EDO but still acceptable (2(18/31) = 1.4955179). The 31 notes can be mapped onto the 35 note names of the Western notational system.
Steps = 31 * log2 (f/f0) where f is the frequency in 31EDO
| note name | interval above C
| steps | cents |
| C | Perfect unison | 0 | 0 |
| C# | Augmented unison | 2 | 77 |
| C## | Doubly augmented unison | 4 | 155 |
| Dbb & B## | Diminished second | 1 | 39 |
| Db | Minor second | 3 | 116 |
| D | Major second | 5 | 194 |
| D# | Augmented second | 7 | 271 |
| D## & Fbb | Doubly augmented second | 9 | 348 |
| Ebb | Diminished third | 6 | 232 |
| Eb | Minor third | 8 | 310 |
| E | Major third | 10 | 387 |
| E# | Augmented third | 12 | 465 |
| Fb | Diminished fourth | 11 | 426 |
| F | Perfect fourth | 13 | 503 |
| F# | Augmented fourth | 15 | 581 |
| F## | Doubly augmented fourth | 17 | 658 |
| Gbb & E## | Doubly diminished fifth | 14 | 542 |
| Gb | Diminished fifth | 16 | 619 |
| G | Perfect fifth | 18 | 697 |
| G# | Augmented fifth | 20 | 774 |
| G## | Doubly augmented fifth | 22 | 852 |
| Abb | Diminished sixth | 19 | 735 |
| Ab | Minor sixth | 21 | 813 |
| A | Major sixth | 23 | 890 |
| A# | Augmented sixth | 25 | 968 |
| A## & Cbb | Doubly augmented sixth | 27 | 1045 |
| Bbb | Diminished seventh | 24 | 929 |
| Bb | Minor seventh | 26 | 1006 |
| B | Major seventh | 28 | 1084 |
| B# | Augmented seventh | 30 | 1161 |
| Cb | Diminished octave | 29 | 1123 |
| C | Perfect octave | 31 | 1200 |
It is undeniable, though, that just intonation should be explored in greater detail and I recommend readers wishing to do this go to The Just Intonation Network (check out the references listed below)
|
|
|
Kyle Gann's Anatomy of An Octave
::

|
Key word:
anatomy of an octave |
| 1 |
For the reference of tuning enthusiasts, we have included an extended and annotated version of
Kyle Gann's Anatomy of An Octave, which contains all pitches that meet any one of the following criteria:
- All ratios between whole numbers 32 and lower
- All ratios between 31-limit numbers up to 64 (31-limit meaning that the numbers contain no prime-number factors larger than 31)
- Harmonics up to 128 (each whole number divided by the closest inferior power of 2) including all ratios between 11-limit numbers up to 128
- All intervals in the equal-tempered scale
- All ratios between 5-limit numbers up to 1024
- Certain historically important ratios such as the schisma and Pythagorean comma
The table is similar to, but much briefer than, that found in Alain Danielou's encyclopedic but long out-of-print Comparative Table of Musical Intervals. | interval ratio | cents equivalent | interval name(s) (if any) |
| (1:1) | 0.000 | tonic, unison, 1st harmonic (fundamental of the harmonic series), normalised 2nd harmonic |
| (4375:4374) | 0.40 | ragisma
[ref. List of Musical Intervals] |
| (2401:2400) | 0.72 | breedsma
[ref. List of Musical Intervals] |
| (21/1200:1) | 1.00 | cent |
| (21/1000:1) | 1.20 | millioctave
[ref. List of Musical Intervals] |
| (32805:32768) | 1.954 | skhisma, schisma ((3 to the 8th/2 to the 12th) x 5/8) (the difference between five octaves and eight justly tuned tuned fifths plus one justly tuned major third; the difference between the Phythagorean and syntonic commas) |
| (353:284) | 3.6 | Mercator's comma, the ratio of 53 pure thirds to 31 octaves |
| ((1+(1/100)log10/(2)):1) | 3.99 | Savart
[ref. List of Musical Intervals] |
| (1224440064:1220703125) | 5.292 | parakleisma |
| (225:224) | 7.712 | septimal kleisma or marvel comma
[ref. List of Musical Intervals] |
| (15625:15552) | 8.107 | kleisma |
| (393216:390625) | 11.445 | Würschmidt comma |
| (126:125) | 13.795 | septimal semicomma or starling comma
[ref. List of Musical Intervals] |
| (121:120) | 14.367 | |
| (100:99) | 17.399 | |
| (99:98) | 17.576 | |
| (2048:2025) | 19.553 | minor comma, diaschisma |
| (81:80) | 21.506 | major comma, syntonic comma, comma of Didymus (difference between four justly tuned perfect fifths and two octaves plus a major third)
There are 55.79763 syntonic commas in the octave |
| (21/53:1) | 22.64 | Arabian comma, Holdrian comma or Holder's comma
[ref. List of Musical Intervals] |
| (531441:524288) | 23.460 | Pythagorean or ditonic comma (312/219) (difference between twelve justly tuned perfect fifths and seven octaves)
There are 51.15087 Pythagorean commas in the octave |
| (65:64) | 26.841 | 65th harmonic |
| (64:63) | 27.264 | septimal comma, comma of Archytas (the difference between the 3-limit or Pythagorean seventh and the harmonic seventh) |
| (20000:19683) | 27.660 | minimal diesis |
| (63:62) | 27.700 | |
| (3125:3072) | 29.614 | small diesis |
| (58:57) | 30.109 | |
| (57:56) | 30.642 | |
| (56:55) | 31.194 | Ptolemy's enharmonic |
| (55:54) | 31.767 | |
| (52:51) | 33.617 | |
| (51:50) | 34.283 | |
| (50:49) | 34.976 | septimal sixth-tone or jubilisma
[ref. List of Musical Intervals] |
| (49:48) | 35.697 | septimal diesis or slendro diesis
[ref. List of Musical Intervals] |
| (46:45) | 38.051 | inferior quarter-tone (Ptolemy) |
| (45:44) | 38.906 | |
| (128:125) | 41.059 | diminished second (16/15 x 24/25), enharmonic diesis (the difference between three justly tuned major thirds and one octave), great diesis, enharmonic diesis (Vincentino), 5-limit diesis, limma |
| (525:512) | 43.408 | enharmonic diesis (Avicenna) |
| (40:39) | 43.831 | difference between major and minor semitones |
| (39:38) | 44.970 | superior quarter-tone (Eratosthenes) |
| (77:75) | 45.561 | |
| (36:35) | 48.770 | superior or septimal quarter-tone
[ref. List of Musical Intervals] |
| (250:243) | 49.166 | maximal diesis |
| (21/24:1) | 50.00 | equal-tempered quarter tone |
| (35:34) | 50.184 | equal temperament (ET) 1/4-tone approximation |
| (34:33) | 51.682 | |
| (50331648:48828125) | 52.504 | |
| (33:32) | 53.273 | 33rd harmonic |
| (32:31) | 54.964 | inferior quarter-tone (Didymus) |
| (125:121) | 56.305 | |
| (31:30) | 56.767 | superior quarter-tone (Didymus) |
| (30:29) | 58.692 | |
| (29:28) | 60.751 | |
| (57:55) | 61.836 | |
| (648:625) | 62.565 | major diesis |
| (28:27) | 62.961 | inferior quarter-tone (Archytas) |
| (80:77) | 66.170 | |
| (27:26) | 65.337 | |
| (26:25) | 67.900 | 1/3-tone (Avicenna) |
| (20480:19683) | 68.719 | comma that is associated with super-Pythagorean temperament |
| (51:49) | 69.259 | |
| (126:121) | 70.100 | |
| (25:24) | 70.672 | minor 5-limit semitone (half-step), chromatic diesis, semitone minimus, lesser or just chromatic semitone, minor chroma
[ref. List of Musical Intervals] |
| (24:23) | 73.681 | |
| (117:112) | 75.612 | |
| (23:22) | 76.956 | |
| (67:64) | 79.307 | 67th harmonic |
| (22:21) | 80.537 | hard semitone (1/2-step) (Ptolemy, Avicenna, Safiud) |
| (21:20) | 84.467 | major diesis, septimal chromatic semitone
[ref. List of Musical Intervals] |
| (81:77) | 87.676 | |
| (20:19) | 88.801 | |
| (256:243) | 90.225 | Pythagorean diatonic semitone (half-step), minor or Pythagorean limma, minor semitone
[ref. List of Musical Intervals] |
| (58:55) | 91.946 | |
| (135:128) | 92.179 | limma ascendant, greater chromatic semitone, semitone medius, chromatic semitone, major chroma |
| (96:91) | 92.601 | |
| (6442450944:6103515625) | 93.563 | |
| (19:18) | 93.603 | |
| (55:52) | 97.104 | |
| (128:121) | 97.364 | |
| (18:17) | 98.955 | equal temperament (ET) semitone (half-step)
(approximation familiar to makers of lutes, who used it when fixing frets on lute fingerboards) |
| (21/12:1) | 100.000 | equal temperament (ET) semitone (half-step), equal-tempered minor second, exact
[ref. List of Musical Intervals] |
| (35:33) | 101.867 | |
| (52:49) | 102.876 | |
| (86:81) | 103.698 | |
| (17:16) | 104.955 | overtone semitone (half-step) |
| (33:31) | 108.237 | |
| (49:46) | 109.377 | |
| (16:15) | 111.731 | major 5-limit semitone (half-step), just diatonic semitone
[ref. List of Musical Intervals] |
| (2187:2048) | 113.685 | apotome or apotome Pythagorica, Pythagorean major semitone, Pythagorean chromatic semitone
the difference between a Pythagorean diatonic semitone and a Pythagorean chromatic semitone is the Pythagorean or ditonic comma |
| (31:29) | 115.458 | |
| (77:72) | 116.234 | |
| (15:14) | 119.443 | Cowell just semitone (half-step), septimal diatonic semitone |
| (29:27) | 123.712 | |
| (14:13) | 128.298 | major semitone |
| (69:64) | 130.229 | 69th harmonic |
| (55:51) | 130.721 | |
| (27:25) | 133.238 | alternate Renaissance semitone (half-step), semitone maximus, minor second, large limma |
| (121:112) | 133.810 | |
| (13:12) | 138.573 | 3/4-tone (Avicenna), minor tone |
| (64:59) | 140.828 | |
| (38:35) | 142.373 | |
| (63:58) | 143.159 | |
| (88:81) | 143.498 | |
| (25:23) | 144.353 | |
| (62:57) | 145.568 | |
| (135:124) | 147.143 | |
| (49:45) | 147.428 | |
| (12:11) | 150.637 | undecimal "median" semitone (1/2-step), lesser undecimal neutral second
[ref. List of Musical Intervals] |
| (59:54) | 153.307 | |
| (35:32) | 155.140 | 35th harmonic |
| (23:21) | 157.493 | |
| (57:52) | 158.940 | |
| (34:31) | 159.920 | |
| (800:729) | 160.897 | |
| (56:51) | 161.915 | |
| (11:10) | 165.004 | greater undemical neutral second
[ref. List of Musical Intervals] |
| (54:49) | 168.213 | |
| (32:29) | 170.423 | |
| (21:19) | 173.268 | |
| (31:28) | 176.210 | |
| (567:512) | 176.646 | |
| (51:46) | 178.636 | |
| (71:64) | 179.697 | 71st harmonic |
| (10:9) | 182.404 | minor whole-tone, just minor tone, smaller step
[ref. List of Musical Intervals] |
| (49:40) | 186.338 | |
| (39:35) | 187.343 | |
| (29:26) | 189.050 | |
| (125:112) | 190.115 | |
| (48:43) | 190.437 | |
| (19:17) | 192.558 | |
| (160:143) | 194.468 | |
| (28:25) | 196.198 | |
| (121:108) | 196.771 | |
| (55:49) | 199.980 | |
| (21/6:1) | 200.000 | equal-tempered whole-tone, exact, equal-tempered major second
[ref. List of Musical Intervals] |
| (64:57) | 200.532 | |
| (9:8) | 203.910 | major whole-tone, major tone, greater step, just major second, sesquioctave, tonus, 5th harmonic (normalised) |
| (62:55) | 207.404 | |
| (44:39) | 208.835 | |
| (35:31) | 210.104 | |
| (26:23) | 212.253 | |
| (112:99) | 213.598 | |
| (17:15) | 216.687 | |
| (25:22) | 221.309 | |
| (58:51) | 222.667 | |
| (256:225) | 222.463 | |
| (33:29) | 223.696 | |
| (729:640) | 225.416 | |
| (57:50) | 226.841 | |
| (73:64) | 227.789 | 73rd harmonic |
| (8:7) | 231.174 | septimal whole-tone, septimal major second
[ref. List of Musical Intervals] |
| (63:55) | 235.104 | |
| (55:48) | 235.677 | |
| (39:34) | 237.527 | |
| (225:196) | 238.886 | |
| (31:27) | 239.171 | |
| (147:128) | 239.607 | |
| (169:147) | 241.449 | |
| (23:20) | 241.961 | |
| (2187:1900) | 243.545 | |
| (38:33) | 244.240 | |
| (144:125) | 244.969 | diminished third (6/5 x 24/25) |
| (121:105) | 245.541 | |
| (15:13) | 247.741 | |
| (52:45) | 250.304 | |
| (37:32) | 251.344 | 37th harmonic |
| (81:70) | 252.680 | |
| (125:108) | 253.076 | |
| (22:19) | 253.805 | |
| (51:44) | 255.592 | |
| (196:169) | 256.596 | consonant interval (Avicenna) |
| (29:25) | 256.950 | |
| (36:31) | 258.874 | |
| (93:80) | 260.677 | |
| (57:49) | 261.816 | |
| (64:55) | 262.368 | |
| (7:6) | 266.871 | septimal minor third, subminor third
the named interval is only approximately equal to 7:6 frequency ratio. In terms of cents, it is 267 cents, a quartertone of size 36/35 flatter than a 5-limit just minor third of 6:5. In the meantone era the interval made its appearance as the alternative minor third in remote keys, under the name augmented second
[ref. List of Musical Intervals] |
| (90:77) | 270.080 | |
| (75:64) | 274.582 | augmented second (9/8 x 25/24) |
| (34:29) | 275.378 | |
| (88:75) | 276.736 | |
| (27:23) | 277.591 | |
| (20:17) | 281.358 | |
| (33:28) | 284.447 | |
| (46:39) | 285.792 | |
| (13:11) | 289.210 | |
| (58:49) | 291.925 | |
| (45:38) | 292.711 | |
| (32:27) | 294.135 | Pythagorean minor third, Pythagorean semiditone |
| (19:16) | 297.513 | overtone minor third |
| (21/4:1) | 300.000 | equal-tempered minor third, exact |
| (25:21) | 301.847 | |
| (31:26) | 304.508 | |
| (105:88) | 305.777 | |
| (55:46) | 309.357 | |
| (6:5) | 315.641 | 5-limit just minor third, sesquiquintan, semiditonus
[ref. List of Musical Intervals] |
| (19683:16384) | 317.595 | |
| (77:64) | 320.144 | 77th harmonic |
| (35:29) | 325.562 | |
| (29:24) | 327.622 | |
| (75:62) | 329.547 | |
| (98:81) | 329.832 | |
| (121:100) | 330.008 | |
| (23:19) | 330.761 | |
| (63:52) | 332.208 | |
| (40:33) | 333.041 | |
| (17:14) | 336.130 | |
| (243:200) | 337.148 | |
| (62:51) | 338.125 | |
| (28:23) | 340.552 | |
| (39:32) | 342.483 | 39th harmonic (major third minus a minor diesis) |
| (128:105) | 342.905 | |
| (8000:6561) | 343.301 | |
| (11:9) | 347.408 | undecimal "median" third, undecimal neutral third
[ref. List of Musical Intervals] |
| (60:49) | 350.617 | |
| (49:40) | 351.338 | |
| (38:31) | 352.477 | |
| (27:22) | 354.547 | |
| (16:13) | 359.472 | |
| (79:64) | 364.537 | 79th harmonic |
| (100:81) | 364.807 | |
| (121:98) | 364.984 | |
| (21:17) | 365.825 | |
| (99:80) | 368.914 | |
| (26:21) | 369.747 | |
| (57:46) | 371.194 | |
| (31:25) | 372.408 | |
| (36:29) | 374.333 | |
| (56:45) | 378.602 | |
| (96:77) | 381.811 | |
| (8192:6561) | 384.360 | Pythagorean "schismatic" third |
| (5:4) | 386.314 | 5-limit just major third, sesquiquartan, ditonus |
| (64:51) | 393.090 | |
| (49:39) | 395.169 | |
| (44:35) | 396.178 | |
| (39:31) | 397.447 | |
| (34:27) | 399.090 | |
| (21/3:1) | 400.000 | equal-tempered major third, exact |
| (63:50) | 400.108 | |
| (121:96) | 400.681 | |
| (29:23) | 401.303 | |
| (125:99) | 403.713 | |
| (24:19) | 404.442 | |
| (512:405) | 405.866 | |
| (62:49) | 407.384 | |
| (81:64) | 407.820 | Pythagorean major third, Pythagorean ditone (that is two 9:8 tones) |
| (19:15) | 409.244 | |
| (33:26) | 412.745 | |
| (80:63) | 413.578 | |
| (14:11) | 417.508 | undecimal major third
[ref. List of Musical Intervals] |
| (51:40) | 420.597 | |
| (125:98) | 421.289 | |
| (23:18) | 424.364 | |
| (32:25) | 427.373 | diminished fourth |
| (41:32) | 429.062 | 41st harmonic |
| (50:39) | 430.145 | major third plus a minor diesis |
| (77:60) | 431.875 | |
| (9:7) | 435.084 | septimal major third, supermajor third
the named interval interval is exactly or approximately equal to a 9:7 frequency ratio. In terms of cents, it is 435 cents, a quartertone of size 36/35 sharper than a just major third of 5/4. In the early meantone era the interval made its appearance as the alternative major third in remote keys, under the name diminished fourth.
[ref. List of Musical Intervals]
|
| (58:45) | 439.353 | |
| (49:38) | 440.139 | |
| (40:31) | 441.278 | |
| (31:24) | 443.081 | |
| (1323:1024) | 443.517 | |
| (128:99) | 444.772 | |
| (22:17) | 446.363 | |
| (57:44) | 448.150 | |
| (162:125) | 448.879 | |
| (35:27) | 449.275 | |
| (83:64) | 450.047 | 83rd harmonic |
| (100:77) | 452.484 | |
| (13:10) | 454.214 | perfect fourth minus a minor diesis |
| (125:96) | 456.986 | augmented third (5/4 x 25/24) |
| (30:23) | 459.994 | |
| (64:49) | 462.348 | |
| (98:75) | 463.069 | |
| (17:13) | 464.428 | |
| (72:55) | 466.278 | |
| (55:42) | 466.851 | |
| (38:29) | 467.936 | |
| (21:16) | 470.781 | septimal fourth |
| (46:35) | 473.135 | |
| (25:19) | 475.114 | |
| (320:243) | 476.539 | |
| (29:22) | 478.259 | |
| (675:512) | 478.492 | |
| (33:25) | 480.646 | |
| (45:34) | 485.286 | |
| (85:64) | 491.269 | 85th harmonic |
| (4:3) | 498.045 | harmonic fourth, just perfect fourth, sesquitertan, sesquitertium, diatessaron
[ref. Pythagorean Intervals] |
| (25/12:1) | 500.000 | equal-tempered perfect fourth, exact |
| (75:56) | 505.757 | |
| (51:38) | 509.397 | |
| (43:32) | 511.518 | 43rd harmonic |
| (121:90) | 512.412 | |
| (39:29) | 512.905 | |
| (35:26) | 514.612 | |
| (66:49) | 515.621 | |
| (31:23) | 516.761 | |
| (27:20) | 519.551 | 5-limit wolf fourth
[ref. List of Musical Intervals] |
| (177147:131072) | 521.505 | |
| (23:17) | 523.319 | |
| (42:31) | 525.745 | |
| (19:14) | 528.687 | |
| (110:81) | 529.812 | |
| (87:64) | 531.532 | 87th harmonic |
| (34:25) | 532.328 | |
| (49:36) | 533.742 | |
| (15:11) | 536.951 | |
| (512:375) | 539.104 | |
| (160/117) | 541.9 | perfect fourth plus a minor diesis |
| (26:19) | 543.015 | |
| (63:46) | 544.462 | |
| (48:35) | 546.815 | |
| (1000:729) | 547.211 | |
| (11:8) | 551.318 | undecimal tritone (11th harmonic) |
| (62:45) | 554.812 | |
| (40:29) | 556.737 | |
| (29:21) | 558.796 | |
| (112:81) | 561.006 | |
| (18:13) | 563.382 | |
| (25:18) | 568.717 | augmented fourth (4/3 x 25/24) |
| (89:64) | 570.880 | 89th harmonic |
| (32:23) | 571.726 | |
| (39:28) | 573.657 | |
| (46:33) | 575.001 | |
| (88:63) | 578.582 | |
| (7:5) | 582.512 | lesser septimal tritone
[ref. List of Musical Intervals] |
| (108:77) | 585.721 | |
| (1024:729) | 588.270 | low Pythagorean tritone |
| (45:32) | 590.224 | high 5-limit tritone (major third plus 9/8 whole tone)
(25:18 if the 10/9 whole tone used instead) |
| (38:27) | 591.648 | |
| (31:22) | 593.718 | |
| (55:39) | 595.149 | |
| (24:17) | 597.000 | |
| (21/2:1) | 600.000 | equal-tempered tritone, exact |
| (99:70) | 600.088 | |
| (17:12) | 603.000 | |
| (44:31) | 606.282 | |
| (125:88) | 607.623 | |
| (27:19) | 608.352 | |
| (91:64) | 609.354 | 91st harmonic |
| (64:45) | 609.776 | low 5-limit tritone |
| (729:512) | 611.730 | high Pythagorean tritone, Tritonus (German)
[ref. Pythagorean Intervals] |
| (57:40) | 613.154 | |
| (77:54) | 614.279 | |
| (10:7) | 617.488 | greater septimal tritone
[ref. List of Musical Intervals] |
| (63:44) | 621.418 | |
| (33:23) | 624.999 | |
| (56:39) | 626.343 | |
| (23:16) | 628.274 | 23rd harmonic |
| (36:25) | 631.283 | diminished fifth (3/2 x 24/25) |
| (121:84) | 631.855 | |
| (49:34) | 632.696 | |
| (75:52) | 634.1 | diminished fifth (tritone plus a minor diesis) |
| (13:9) | 636.618 | |
| (81:56) | 638.994 | |
| (55:38) | 640.119 | |
| (42:29) | 641.204 | |
| (29:20) | 643.263 | |
| (45:31) | 645.188 | |
| (93:64) | 646.991 | 93rd harmonic |
| (16:11) | 648.682 | inversion of eleventh harmonic |
| (51:35) | 651.771 | |
| (729:500) | 652.789 | |
| (35:24) | 653.185 | |
| (19:13) | 656.985 | |
| (117:80) | 658.1 | perfect fifth minus a minor diesis |
| (375:256) | 660.896 | |
| (22:15) | 663.049 | |
| (47:32) | 665.507 | 47th harmonic |
| (72:49) | 666.258 | |
| (25:17) | 667.672 | |
| (81:55) | 670.188 | |
| (28:19) | 671.313 | |
| (31:21) | 674.255 | |
| (189:128) | 674.691 | |
| (34:23) | 676.681 | |
| (262144:177147) | 678.495 | wolf fifth, the interval between G# and Ed in early Pythagorean chromatic tuning, a fifth containing (i.e. narrowed by) the whole of a Pythagorean or ditonic comma (531441:524288) |
| (40:27) | 680.449 | (dissonant) 5-limit wolf fifth
[ref. List of Musical Intervals] |
| (46:31) | 683.239 | |
| (95:64) | 683.827 | 95th harmonic |
| (49:33) | 684.379 | |
| (52:35) | 685.388 | |
| (58:39) | 687.095 | |
| (125:84) | 688.160 | |
| (112:75) | 694.243 | |
| (121:81) | 694.816 | |
| (27/12:1) | 700.000 | equal-tempered perfect fifth, exact |
| (3:2) | 701.955 | harmonic fifth, just perfect fifth, trihemitone, diapente, sesquialterum, 3rd harmonic
[ref. List of Musical Intervals]
[ref. Pythagorean Intervals] |
| (121:80) | 716.322 | |
| (50:33) | 719.354 | |
| (97:64) | 719.895 | 97th harmonic |
| (1024:675) | 721.508 | |
| (44:29) | 721.741 | |
| (243:160) | 723.461 | |
| (38:25) | 724.886 | |
| (35:23) | 726.865 | |
| (32:21) | 729.219 | |
| (29:19) | 732.064 | |
| (84:55) | 733.149 | |
| (55:36) | 733.722 | |
| (26:17) | 735.572 | |
| (75:49) | 736.931 | |
| (49:32) | 737.652 | 49th harmonic |
| (23:15) | 740.006 | |
| (192:125) | 743.014 | diminished sixth (8/5 x 24/25) |
| (20:13) | 745.786 | perfect fifth plus a minor diesis |
| (77:50) | 747.516 | |
| (54:35) | 750.725 | |
| (125:81) | 751.121 | |
| (17:11) | 753.637 | |
| (99:64) | 755.228 | 99th harmonic |
| (48:31) | 756.919 | |
| (31:20) | 758.722 | |
| (45:29) | 760.647 | |
| (14:9) | 764.916 | septimal minor sixth |
| (120:77) | 768.125 | |
| (39:25) | 769.855 | minor sixth minus a minor diesis |
| (25:16) | 772.627 | augmented fifth |
| (36:23) | 775.636 | |
| (11:7) | 782.492 | undecimal minor sixth |
| (63:40) | 786.422 | |
| (52:33) | 787.255 | |
| (101:64) | 789.854 | 101st harmonic |
| (30:19) | 790.756 | |
| (128:81) | 792.180 | Pythagorean minor sixth |
| (49:31) | 792.616 | |
| (405:256) | 794.134 | |
| (19:12) | 795.558 | |
| (46:29) | 798.697 | |
| (100:63) | 799.892 | |
| (22/3:1) | 800.000 | equal-tempered minor sixth, exact |
| (27:17) | 800.910 | |
| (62:39) | 802.553 | |
| (35:22) | 803.822 | |
| (51:32) | 806.910 | 51st harmonic |
| (8:5) | 813.686 | 5-limit just minor sixth (inversion of 5-limit just major third) |
| (6561:4096) | 815.640 | Pythagorean "schismatic" sixth |
| (77:48) | 818.189 | |
| (45:28) | 821.398 | |
| (103:64) | 823.801 | 103rd harmonic |
| (29:18) | 825.667 | |
| (50:31) | 827.592 | |
| (121:75) | 828.053 | |
| (21:13) | 830.253 | |
| (55:34) | 832.676 | |
| (34:21) | 834.175 | |
| (81:50) | 835.193 | |
| (125:77) | 838.797 | |
| (13:8) | 840.528 | overtone sixth |
| (57:35) | 844.328 | |
| (44:27) | 845.453 | |
| (31:19) | 847.523 | |
| (80:49) | 848.662 | |
| (49:30) | 849.383 | |
| (18:11) | 852.592 | undecimal "median" sixth, undecimal neutral sixth
[ref. List of Musical Intervals] |
| (105:64) | 857.095 | 105th harmonic |
| (64:39) | 857.517 | minor sixth plus a minor diesis |
| (23:14) | 859.448 | |
| (51:31) | 861.875 | |
| (400:243) | 862.852 | |
| (28:17) | 863.870 | |
| (33:20) | 866.959 | |
| (38:23) | 869.239 | |
| (81:49) | 870.168 | |
| (48:29) | 872.378 | |
| (53:32) | 873.505 | 53rd harmonic |
| (58:35) | 874.438 | |
| (63:38) | 875.223 | |
| (128:77) | 879.856 | |
| (107:64) | 889.760 | 107th harmonic |
| (5:3) | 884.359 | 5-limit just major sixth (inversion of a 5-limit just minor third) |
| (57:34) | 894.513 | |
| (52:31) | 895.492 | |
| (42:25) | 898.153 | |
| (121:72) | 898.726 | |
| (23/4:1) | 900.000 | equal-tempered major sixth, exact |
| (32:19) | 902.487 | |
| (27:16) | 905.865 | Pythagorean major sixth |
| (49:29) | 908.075 | |
| (22:13) | 910.790 | |
| (39:23) | 914.208 | |
| (56:33) | 915.553 | |
| (17:10) | 918.642 | |
| (109:64) | 921.821 | 109th harmonic |
| (46:27) | 922.409 | |
| (75:44) | 923.264 | |
| (29:17) | 924.622 | |
| (128:75) | 925.418 | diminished seventh (16/9 x 24/25) |
| (77:45) | 929.920 | |
| (12:7) | 933.129 | septimal major sixth (inversion of a minimal third) |
| (55:32) | 937.632 | 55th harmonic |
| (31:18) | 941.126 | |
| (441:256) | 941.562 | |
| (50:29) | 943.050 | |
| (19:11) | 946.195 | |
| (216:125) | 946.924 | |
| (121:70) | 947.496 | |
| (45:26) | 949.696 | |
| (26:15) | 952.259 | |
| (111:64) | 953.299 | 111th harmonic |
| (125:72) | 955.031 | augmented sixth (5/3 x 25/24) |
| (33:19) | 955.760 | |
| (40:23) | 958.039 | |
| (54:31) | 960.829 | |
| (96:55) | 964.323 | |
| (110:63) | 964.896 | |
| (7:4) | 968.826 | septimal minor seventh, harmonic seventh, (inversion of major tone)
[some assert that 7:4 is one of the blue notes used in jazz] |
| (58:33) | 976.304 | |
| (225:128) | 976.537 | 225th harmonic |
| (51:29) | 977.333 | |
| (44:25) | 978.691 | |
| (30:17) | 983.313 | |
| (113:64) | 984.215 | 113th harmonic |
| (99:56) | 986.402 | |
| (23:13) | 987.747 | |
| (62:35) | 989.896 | |
| (39:22) | 991.165 | |
| (55:31) | 992.596 | |
| (16:9) | 996.090 | Pythagorean small minor seventh, lesser just minor seventh, dominant seventh
(one of the inversions of a whole tone, the other being 9:5) |
| (57:32) | 999.468 | 57th harmonic |
| (25/6:1) | 1000.000 | equal-tempered minor seventh |
| (98:55) | 1000.020 | |
| (25:14) | 1003.802 | |
| (34:19) | 1007.442 | |
| (52:29) | 1010.950 | |
| (88:49) | 1013.666 | |
| (115:64) | 1014.588 | 115th harmonic |
| (9:5) | 1017.596 | 5-limit large minor seventh, greater just minor seventh, tonic seventh
(one of the inversions of a whole tone, the other being 16:9) |
| (59049:32768) | 1019.550 | |
| (56:31) | 1023.790 | |
| (38:21) | 1026.732 | |
| (29:16) | 1029.577 | 29th harmonic |
| (49:27) | 1031.787 | |
| (20:11) | 1034.996 | lesser undecimal neutral seventh
[ref. List of Musical Intervals] |
| (51:28) | 1038.085 | |
| (729:400) | 1039.103 | |
| (31:17) | 1040.080 | |
| (42:23) | 1042.507 | |
| (117:64) | 1044.438 | 117th harmonic |
| (64:35) | 1044.860 | |
| (4000:2187) | 1045.256 | |
| (11:6) | 1049.363 | undecimal "median" seventh, greater undecimal neutral seventh
[ref. List of Musical Intervals] |
| (90:49) | 1052.572 | |
| (57:31) | 1054.432 | |
| (46:25) | 1055.647 | |
| (81:44) | 1056.502 | |
| (35:19) | 1057.627 | |
| (59:32) | 1059.172 | 59th harmonic |
| (24:13) | 1061.427 | inversion of minor tone |
| (50:27) | 1066.762 | |
| (63:34) | 1067.780 | |
| (13:7) | 1071.702 | inversion of major semitone |
| (119:64) | 1073.781 | 119th harmonic |
| (54:29) | 1076.288 | |
| (28:15) | 1080.557 | |
| (58:31) | 1084.542 | |
| (15:8) | 1088.269 | 5-limit just major seventh |
| (62:33) | 1091.763 | |
| (32:17) | 1095.045 | |
| (49:26) | 1097.124 | |
| (66:35) | 1098.133 | |
| (211/12:1) | 1100.000 | equal-tempered major seventh, exact |
| (17:9) | 1101.045 | |
| (121:64) | 1102.636 | 121st harmonic |
| (125:66) | 1105.668 | |
| (36:19) | 1106.397 | |
| (256:135) | 1107.821 | |
| (55:29) | 1108.054 | |
| (243:128) | 1109.775 | Pythagorean major seventh |
| (19:10) | 1111.199 | |
| (40:21) | 1115.533 | inversion of minor semitone/major diesis |
| (61:32) | 1116.885 | 61st harmonic |
| (21:11) | 1119.463 | |
| (44:23) | 1123.044 | |
| (23:12) | 1126.319 | |
| (48:25) | 1129.328 | diminished octave |
| (121:63) | 1129.900 | |
| (123:64) | 1131.017 | 123rd harmonic |
| (25:13) | 1132.100 | |
| (77:40) | 1133.830 | |
| (52:27) | 1134.663 | |
| (27:14) | 1137.039 | septimal major seventh |
| (56:29) | 1139.249 | |
| (29:15) | 1141.308 | |
| (60:31) | 1143.233 | |
| (31:16) | 1145.036 | 31st harmonic |
| (64:33) | 1146.727 | |
| (33:17) | 1148.318 | |
| (243:125) | 1150.834 | |
| (39:20) | 1156.169 | inversion of minor diesis |
| (125:64) | 1158.941 | augmented seventh (15/8 x 25/24) |
| (88:45) | 1161.094 | |
| (45:23) | 1161.991 | |
| (96:49) | 1164.303 | |
| (49:25) | 1165.024 | |
| (51:26) | 1166.383 | |
| (108:55) | 1168.233 | |
| (55:28) | 1168.806 | |
| (57:29) | 1169.891 | |
| (63:32) | 1172.736 | 63rd harmonic |
| (160:81) | 1178.494 | |
| (99:50) | 1182.601 | |
| (125:63) | 1186.205 | |
| (127:64) | 1186.422 | 127th harmonic |
| (2:1) | 1200.000 | octave, diapason, 2nd harmonic (which normalizes to 1:1, i.e. the 1st harmonic or fundamental) |
| useful intervals that exceed the octave |
| (32:15) | 1311.731 | minor ninth |
| (9:4) | 1403.910 | major ninth |
| (7:3) | 1466.871 | harmonic minor tenth |
| (12:5) | 1515.641 | minor ninth |
| (5:2) | 1586.314 | major ninth |
| (8:3) | 1698.045 | perfect eleventh |
| (11:4) | 1751.318 | harmonic eleventh |
| (45:16) | 1790.224 | augmented eleventh |
| (3:1) | 1901.955 | just perfect twelfth, tritave |
| (25:8) | 1972.627 | augmented twelfth |
| (16:5) | 2013:686 | minor thirteenth |
| (13:4) | 2040.528 | harmonic thirteenth |
| (10:3) | 2084.359 | major thirteenth |
| (7:2) | 2168.826 | harmonic fourteenth |
| (32:9) | 2196.090 | dominant thirteenth |
| (18:5) | 2217.596 | tonic fourteenth |
| (15:4) | 2288.269 | major fourteenth |
| (4:1) | 2400.000 | double octave, fifteenth |
References:
|
|
|
Naming Intervals
::

|
Key word:
intervals |
| 1 |
Naming Intervals
The following table lists the names of the most common intervals using a number of modern conventions.
The standard system for comparing intervals of different sizes is with cents, based on a logarithmic scale where the octave is divided into 1200 equal parts. In equal temperament, each semitone is exactly 100 cents. To remind our readers of the formula given earlier, the value in cents for the interval f1 to f2 is 1200×log2(f2/f1).
In diatonic set theory, specific and generic intervals are distinguished. Specific intervals are the interval class or number of semitones between scale degrees or collection members, and generic intervals are the number of scale steps between notes of a collection or scale.
# semitones
|
Interval
class |
Generic
interval |
Common
diatonic name |
Comparison of interval width in cents (to nearest integer) |
5-limit
just
intonation |
Pythagorean
3-limit just intonation |
quarter-comma
meantone |
equal
temperament |
| 0 |
0 |
0 |
perfect unison |
(1:1) | 0 |
(1:1) | 0 |
0 |
0 |
| 1 |
1 |
1 |
minor second |
(16:15) | 112 |
(256:243) | 90 |
117 |
100 |
| 2 |
2 |
1 |
major second |
(9:8) | 204 |
(9:8) | 204 |
193 |
200 |
| 3 |
3 |
2 |
minor third |
(6:5) | 316 |
(32:27) | 294 |
310 |
300 |
| 4 |
4 |
2 |
major third |
(5:4) | 386 |
(81:64) | 408 |
386 |
400 |
| 5 |
5 |
3 |
perfect fourth |
(4:3) | 498 |
(4:3) | 498 |
503 |
500 |
| 6 |
6 |
3 |
augmented fourth |
(45:32) | 590 |
(729:512) | 612 |
579 |
600 |
| 4 | diminished fifth | (64:45) | 610 | 621 |
| 7 |
5 |
4 |
perfect fifth |
(3:2) | 702 |
(3:2) | 702 |
697 |
700 |
| (wolf fifth) 737 |
| 8 |
4 |
5 |
minor sixth |
(8:5) | 814 |
(128:81) | 792 |
814 |
800 |
| 9 |
3 |
5 |
major sixth |
(5:3) | 884 |
(27:16) | 906 |
889 |
900 |
| 10 |
2 |
6 |
minor seventh |
(16:9) | 996 |
(16:9) | 996 |
1007 |
1000 |
| 11 |
1 |
6 |
major seventh |
(15:8) | 1088 |
(243:128) | 1110 |
1083 |
1100 |
| 12 |
0 |
0 |
perfect octave |
(2:1) | 1200 |
(2:1) | 1200 |
1200 |
1200 |
Reference:
Interval (music)
Interval calculator that converts frequency ratios to cents
|
|
|
Historical Temperaments
::

|
Key word:
historical temperaments |
| 1 |
Historical Temperaments
|
It would be useful to explain some of the terms we use below.
To raise a note through one octave, we multiply the frequency by 2, while, conversely, to lower a note by one octave, we multiply the frequency by 1/2 (which is the same as dividing it by 2). If A=440 Hz, then the A one octave above has the frequency 880 Hz while the A one octave below has the frequency 220 Hz. Because a note bearing the same name lying in any octave is considered a member of the same pitch class, no matter how many times we halve or double the frequency, the pitch class remains the same. These doublings or halvings are the process we have called 'normalisation'. Without changing its pitch class, any note can be 'normalised' so that it lies within a frequency range covered by a particular octave.
The pure 5th to any note may be found by multiplying that note's frequency by 3/2. So, if A=440 Hz, the pure 5th above it has the frequency 660 Hz. If we want to narrow the interval we must multiply the frequency of the 5th by a number that is less than 1, while, conversely, if we want to widen the interval, we multiply the frequency of the 5th by a number that is greater than 1. Of course, we can also widen an interval by lowering the frequency of the lower note, or narrow it by raising the frequency of the lower note.
The Pythagorean comma (also called the ditonic comma) is the interval by which a note that is 12 pure 5ths above a particular note and which has been normalised to lie within an octave of that note, exceeds the original note. Mathematically, it is the fractional interval 531441/524288. If we want to narrow the interval of a 5th by lowering the upper note by a Pythagorean comma, we must multiply the frequency of the pure 5th by the inverse of the comma, i.e. by the fraction 524288/531441.
Fractions of a comma can be understood as roots of the comma itself. Thus, if, as in equal temperament, each of the 12 5ths is narrowed by 1/12 of the comma, and we know that applying this factor 12 times is equivalent to narrowing a single 5th by 1 comma, we should expect the multiplier to be the 12th root of the comma, written by mathematicians in the form (524288/531441)^(1/12). By an identical logic, narrowing an interval by 1/4 of a comma requires the application of the 4th root of the comma and narrowing it by 1/3 of a comma, the application of the 3rd root. To widen an interval by 1/4 comma we use the 4th root of the inverse of the comma, i.e. (531441/524288)^(1/4), and so on.
It is common to find this narrowing and widening notated by the use of positive or negative fractions: thus, -1/4, indicates a narrowing by 1/4 of a comma, -1/12 indicates a narrowing by 1/12 of a comma while +1/4 indicates a widening of an interval by 1/4 of a comma. 0 indicates that the interval is pure or just. However, it should be noted that some early sources are unclear which of the two most commonly used commas they mean to apply, i.e. whether the Pythagorean (531441:524288) or the syntonic (81:80), and in some cases whether they intend one for one particular tempering and the other for a different tempering. Obviously, in all cases, the final result must find the interval Eb-D# narrowed to zero. Although in the tables below we have used only the Pythagorean comma, in regular meantone temperaments where the tempering of the fifth is expressed in a fraction of a comma, the comma is most usually the syntonic. In well-temperaments, like Werckmeister's, where the cycle of fifths closes in a circle, the temperings are usually expressed in fractions of a Pythagorean comma.
|
Prior to the almost universal adoption of the equal temperament system of tuning where the interval between successive semitones is a constant and the ratio for the octave is set at 2:1, musicians and theorists produced numerous solutions for bending the natural Pythagorean scale to practical use. That this was an impossible task, particularly if one wished to modulate to all the possible major or minor scales, was demonstrated time and again by composers such as Willaert who used their works to demonstrate the shortcomings of any of the temperaments then in use. Written in four parts, the vocal work Quid non ebrietas, starts on the key note before taking the singers through a sequence of perfect fifths that, if they use Pythagorean tuning based on perfect fifths, leaves them sharp by the Pythagorean comma when they return to the key note at the end of the piece. If the singers choose instead to use just intonation, they reach the end flat to the desired key note. Of course, most of these problems could be ignored so long as composers chose to remain reasonably close to the key in which the work started. Composers like Willaerts, Nicola Vicentino and Carlo Gesualdo pushed the boundaries of temperament so hard that special instruments had to be invented to handle the complexities of tempered scales as key notes changed. Vicentino invented the archicembalo with its six rows of keys. He also inspired Fabio Colonna's sambuca in which the octave was divided into thirty-one parts.
The temperaments we set out below were commonly used before the widespread introduction of equal temperament. Each was an attempt to rid the 'so-called' natural scale of its problems under modulation. We give some information below about the common 'historical temperaments' used when setting keyboard instruments for historically informed performance all calculations based on a'=440 Hz. We have also provided a calculator below which provides many temperaments at historical pitches where a' is lower or higher than 440 Hz.
|
| 2 |
Pythagorean
Strictly, not a temperament but a tuning because natural intervals are not adjusted but allowed to fall where they may, it dates back to 500 BC. This simple scale creates eleven pure fifths around the circle, leaving the entire Pythagorean comma between G# and Eb There are four pure major thirds at B-D#, F#-A#, Db-F, and Ab-C, but these are not particularly useful. The remainder are quite harsh.
| pure 5ths tuning (each 5th up, multiply by 3/2 & normalise; each 5th down multiply by 2/3 & normalise) |
| note name: |
Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | D# |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 371.250 | 278.438 | 417.656 | 626.484 |
| with pure 5ths, high D# is sharp to low Eb (for enharmonic equivalence, the ratio of frequencies must be that of a pure octave, i.e. 2:1) |
Pythagorean tuning in key of C: the whole Pythagorean comma is placed in the interval G#-D#;
multiply frequency of high D# by 524288/531441, i.e. narrow the fifth between G# and D# by one Pythagorean comma, and the octave is now pure |
| note name: |
Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 371.250 | 278.438 | 417.656 | 618.052 |
| with Pythagorean tuning, interval between of high and low Eb is a pure octave (ratio is 2:1) |
| from which calculation, the required Pythagorean scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 260.741 | 278.438 | 293.333 | 309.026 | 330.000 | 347.654 | 371.250 | 391.111 | 417.656 | 440.000 | 463.539 | 495.000 |
Those who are paying attention may have noticed that when we tune with pure 5ths the last note in the series, D#, when normalised lies above the Eb at the beginning. However, on modern keyboard instruments, D# and Eb are enharmonically equivalent (that is, they are played with the same key). Some may even be aware that under some tuning systems D# lies below Eb. How can this be?
Clavichord maker Peter Bavington, explains:
|
The truth is that in 'just intonation' with pure major thirds D# would be below Eb (the discrepancy is about 35.69 cents), but in what Barbieri calls 'Pythagorean-expressive' intonation it is the other way round: D# lies above Eb (by the Pythagorean comma of 23.46 cents). He documents the change, occurring around 1750 and the years after: at that time teachers still thought of the whole tone as consisting of nine parts ('commas' as they called them) whereas before 1750 the chromatic semitone (D-D#) was regarded as having four and
the diatonic (D#-E) five. Later people began to put them the other way round so that D-D# has five commas and D#-E only four - an example of the raising of the leading note. Similarly Eb-E natural now had five commas, so as to bring the Eb closer to D.
I remember attending a lecture at Morley College ages ago on microtonal music, where the lecturer convincingly demonstrated with recordings that (modern) violinists playing, say, D-Eb-D narrowed the semitone to about 1/3 of an equal temperament whole-tone. I suspect they do this sort of thing all the time when playing melodies, but at cadences and in slow passages revert to the older 'harmonic' intonation where they have a sustained note making a third or sixth with the bass (which I think is actually not all that often).
So, to summarize, D# is sometimes above and sometimes below Eb, depending on style and many other things. It is only on our inflexible keyboards that we are forced to choose!
|
|
| 3 |
van Zwolle
Arnout van Zwolle (1400-1466) modified the Pythagorean scale by placing the comma in the interval B-F#. This moved the thirds to D-F#, A-C#, E-G#, and B-Eb, which were more useful. This gives pure major triads on D, A and E.
| pure 5ths tuning (each 5th up, multiply by 3/2 & normalise; each 5th down multiply by 2/3 & normalise) |
| note name: | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | D# |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 371.250 | 278.438 | 417.656 | 626.484 |
| with pure 5ths, high D# is sharp to low Eb (for enharmonic equivalence, the ratio of frequencies must be that of a pure octave, i.e. 2:1) |
van Zwolle tuning in key of C: the whole Pythagorean comma is placed in the interval B-F#;
multiply frequency of F# by 524288/531441, i.e. narrow the fifth B-F# by one Pythagorean comma, and then continue upwards in pure 5ths |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 366.253 | 274.690 | 412.035 | 618.052 |
| from which calculation, the required van Zwolle scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 260.741 | 274.690 | 293.333 | 309.026 | 330.000 | 347.654 | 366.250 | 391.111 | 412.035 | 440.000 | 463.539 | 495.000 |
|
| 4 |
Meantone
The best known of the old scales, this scale emphasizes pure thirds by making the fifths narrow. It was certainly in use by the end of the fifteenth century, if not earlier. All whole steps are equally spaced, one half of a major third apart. It also has a very prominent "wolf" between G# and Eb. If the circle is extended down to Ab, the pitch is very different from the G#. Some baroque keyboards had a split pair of black keys that allowed the musician to choose G# or Ab. G# is set two perfect thirds above the lower C and so its ratio is 25:16. Ab is set a perfect third below the higher (octave) C and its ratio is 8:5.
| pure 5ths tuning (each 5th up, multiply by 3/2 & normalise; each 5th down multiply by 2/3 & normalise) |
| note name: | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | D# |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 371.250 | 278.438 | 417.656 | 626.484 |
| with pure 5ths, high D# is sharp to low Eb (for enharmonic equivalence, the ratio of frequencies must be that of a pure octave, i.e. 2:1) |
1/4 comma meantone tuning in key of C: the Pythagorean comma is spread by narrowing every 5th by a 1/4 of the comma, except that the 5th G#-D#/Eb is widened by 7/4 of the comma
multiply every 5th by (524288/531441)^(1/4), except that between G# and D#/Eb which is multiplied by (531441/524288)^(7/4) |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 315.372 | 471.458 | 352.397 | 263.404 | 393.770 | 294.329 | 440.000 | 328.884 | 491.657 | 367.496 | 274.690 | 410.641 | 630.744 |
| from which calculation, the 1/4 comma meantone temperament scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 263.404 | 274.690 | 294.329 | 315.372 | 328.884 | 352.397 | 367.496 | 393.770 | 410.641 | 440.000 | 471.458 | 491.657 |
|
| 5 |
Silbermann I, II
Organ builder Gottfried Silbermann (1678-1734) tried several variants to narrow the "wolf" and make his instruments useable in more keys. None of the intervals of these two scales is pure.
| pure 5ths tuning (each 5th up, multiply by 3/2 & normalise; each 5th down multiply by 2/3 & normalise) |
| note name: | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | D# |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 371.250 | 278.438 | 417.656 | 626.484 |
| with pure 5ths, high D# is sharp to low Eb (for enharmonic equivalence, the ratio of frequencies must be that of a pure octave, i.e. 2:1) |
Silbermann I 1/6 comma temperament in key of C: the Pythagorean comma is spread by narrowing every 5th by a 1/6 of the comma, except that the 5th G#-D#/Eb is widened by 5/6 of the comma
multiply every 5th by (524288/531441)^(1/6), except G#-D#/Eb which is multiplied by (531441/524288)^(5/6) |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 313.242 | 468.803 | 350.809 | 262.513 | 392.882 | 293.997 | 440.000 | 329.256 | 492.769 | 368.743 | 275.933 | 412.966 | 626.484 |
| from which calculation, the 1/6 comma temperament Silbermann I scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 262.513 | 275.933 | 293.997 | 313.242 | 329.242 | 350.809 | 368.743 | 392.882 | 412.966 | 440.000 | 468.803 | 492.769 |
Silbermann II 1/6 comma temperament in key of C: the Pythagorean comma is spread by narrowing every 5th by a 1/6 of the comma, except that the 5th G#-D#/Eb is increased by 1/2 of the comma and the 5th Eb-Bb which is increased by a 1/6 of the comma
multiply every 5th by (524288/531441)^(1/6), except G#-D#/Eb which is multiplied by (531441/524288)^(1/2) and Eb-Bb which is multiplied by (531441/524288)^(1/6) |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 311.830 | 468.803 | 350.809 | 262.513 | 392.882 | 293.997 | 440.000 | 329.256 | 492.769 | 368.743 | 275.933 | 412.966 | 623.660 |
| from which calculation, the 1/6 comma temperament Silbermann II scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 262.513 | 275.933 | 293.997 | 311.830 | 329.256 | 350.809 | 368.743 | 392.882 | 412.966 | 440.000 | 468.803 | 492.769 |
|
| 6 |
Rameau
Jean Phillipe Rameau (1683-1764) modified the meantone scale to provide three pure fifths. This very pleasant scale almost completely eliminates the harsh "wolf" of the meantone while preserving most of its pure harmony.
| pure 5ths tuning (each 5th up, multiply by 3/2 & normalise; each 5th down multiply by 2/3 & normalise) |
| note name: | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | D# |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 371.250 | 278.438 | 417.656 | 626.484 |
| with pure 5ths, high D# is sharp to low Eb (for enharmonic equivalence, the ratio of frequencies must be that of a pure octave, i.e. 2:1) |
| Rameau temperament in key of C: the 5ths B-F#, F#-C# and C#-G# are pure, the 5ths Eb-Bb, and F-C are widened (by a 1/3 of a comma) while the remainder are narrowed (all by 1/4 of a comma except Gb-D#/Ed which is narrowed by 1/6 of a comma) |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 310.425 | 467.746 | 352.397 | 263.404 | 393.770 | 294.329 | 440.000 | 328.884 | 491.657 | 368.743 | 276.557 | 414.836 | 620.850 |
| from which calculation, the required Rameau temperament scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 263.404 | 276.557 | 294.329 | 310.425 | 328.884 | 352.397 | 368.743 | 393.770 | 414.836 | 440.000 | 467.746 | 491.657 |
|
| 7 |
Werkmeister I(III), II(IV), III(V), IV(VI)
Organ builder and mathematician Andreas Werkmeister (1645-1706) devoted much of his life to the study of temperament and suggested many, different scales. His goal was to place the best thirds in those keys with the fewest incidentals. It is very likely that Bach (l685-1750) wrote his famous Das Wohltemperierte Klavier, 48 preludes and fugues, for one of these temperaments. The tuning systems are confusingly numbered in two different ways: the first refers to the order in which they were presented as "good temperaments" in Werckmeister's 1691 treatise, the second to their labelling on his monochord. The monochord labels start from III since just intonation is labelled I and quarter-comma meantone is labelled II. Werckmeister IV (VI), the 'so-called' Septenarius tuning is based on a division of the monochord length into 196 parts. Werckmeister I (III) (1/4 ditonic or Pythagorean comma) is one of the three temperaments most commonly used in HIP performance today.
| pure 5ths tuning (each 5th up, multiply by 3/2 & normalise; each 5th down multiply by 2/3 & normalise) |
| note name: | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | D# |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 371.250 | 278.438 | 417.656 | 626.484 |
| with pure 5ths, high D# is sharp to low Eb (for enharmonic equivalence, the ratio of frequencies must be that of a pure octave, i.e. 2:1) |
| Werkmeister I (III) temperament in key of C: the 5ths C-G, G-D,D-A and B-F# are narrowed by 1/4 of the comma while the remainder are pure |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 312.183 | 468.274 | 351.206 | 263.404 | 393.770 | 294.329 | 440.000 | 330.000 | 495.000 | 369.994 | 277.496 | 414.244 | 624.366 |
| from which calculation, the required Werkmeister I (III) temperament scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 263.404 | 277.496 | 294.329 | 312.183 | 330.000 | 351.206 | 369.994 | 393.770 | 416.244 | 440.000 | 468.274 | 495.000 |
| Werkmeister II (IV) temperament in key of C: the 5ths Bb-F, C-G, D-A, E-B and F#-C# are narrowed by 1/3 of the comma; the 5ths Eb-Bb and G#-D# are widened by a 1/3 of a comma while the remainder are pure |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 311.830 | 469.863 | 350.809 | 263.107 | 392.882 | 294.661 | 440.000 | 330.000 | 492.769 | 369.577 | 275.933 | 413.900 | 623.660 |
| from which calculation, the required Werkmeister II (IV) temperament scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 263.107 | 275.933 | 294.661 | 311.830 | 330.000 | 350.809 | 369.577 | 392.882 | 413.900 | 440.000 | 469.863 | 492.769 |
| Werkmeister III (V) temperament in key of C: the 5ths F-C, D-A, A-E, F#-C# and C#-G# are narrowed by 1/4 of the comma; the 5th G#-D# is widened by a 1/4 of a comma while the remainder are pure |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 311.127 | 466.690 | 350.018 | 261.626 | 392.483 | 294.329 | 440.000 | 328.884 | 493.326 | 369.994 | 276.557 | 413.433 | 622.254 |
| from which calculation, the required Werkmeister III (V) temperament scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 261.626 | 276.557 | 294.329 | 311.127 | 328.884 | 350.018 | 369.994 | 392.438 | 413.433 | 440.000 | 466.690 | 493.326 |
References:
|
| 8 |
Kirnberger II, III
Composer and music theorist Johann Philipp Kirnberger (1721-1783) suggested several temperaments. The two scales here offer a large number of pure fifths. The first has pure thirds at C-E, G-B, and D-F# but the fifths at D-A and A-E are somewhat harsh. Kirnberger later proposed an alternate scale with smoother fifths, but only one pure third at C-E. Kirnberger III (1/5 ditonic or Pythagorean comma) is one of the three temperaments most commonly used in HIP performance today.
| pure 5ths tuning (each 5th up, multiply by 3/2 & normalise; each 5th down multiply by 2/3 & normalise) |
| note name: | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | D# |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 371.250 | 278.438 | 417.656 | 626.484 |
| with pure 5ths, high D# is sharp to low Eb (for enharmonic equivalence, the ratio of frequencies must be that of a pure octave, i.e. 2:1) |
| Kirnberger II in key of C: the 5ths D-A and A-E are narrowed by 1/2 of the Pythagorean comma; the remainder are pure |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 311.127 | 466.690 | 350.018 | 262.513 | 393.770 | 295.328 | 440.000 | 327.772 | 491.657 | 368.743 | 276.557 | 414.836 | 622.254 |
| from which calculation, the required Kirnberger II temperament scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 262.513 | 276.557 | 295.328 | 311.127 | 327.772 | 350.018 | 368.743 | 393.770 | 414.836 | 440.000 | 466.690 | 491.657 |
| Kirnberger III in key of C: the 5ths C-G, G-D, D-A and A-E are narrowed by 1/4 of the Pythagorean comma; the remainder are pure |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 312.183 | 468.274 | 351.206 | 263.404 | 393.770 | 294.329 | 440.000 | 328.884 | 493.326 | 369.994 | 277.496 | 416.244 | 624.366 |
| from which calculation, the required Kirnberger III temperament scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 263.404 | 277.496 | 294.329 | 312.183 | 328.884 | 351.206 | 369.994 | 393.770 | 416.244 | 440.000 | 468.274 | 493.326 |
|
| 9 |
Vallotti-Young
Francesco Antonio Vallotti (1697-1780) published his Trattato della scienza teorica e pratica della moderna musica in 1779 although claiming that his theories were set out over 50 years earlier. Discussion of the temperament that bears his name appears in Book 2. Vallotti's temperament was mentioned in England by William Jones in 1781 (Physiological Disquisitions) with a reference to an endorsement by Tartini, who was leader of the professional orchestra in Padua under Vallotti's direction. Thomas Young (1773-1829) was a polymath whose temperament was given as part of an address to the Royal Society in January, 1800 (Philosophical Transactions, pp. 143-47). Young #2 (1800) (1/5 ditonic or Pythagorean comma) is one of the three temperaments most commonly used in HIP performance today.
Kyle Gann in his An Introduction to Historical Tunings, writes: "Thomas Young's Well Temperament [is considered by some] to be the most elegant well temperament, with a fluid variety of tonal colors and a symmetry that matches the piano keyboard: all intervals are symmetrical around D and G# - that is, D-F# and D-Bb are the same size, G#-F# and Ab-Bb the same size, and so on. This is a subtle tuning, quite usable in all keys, and the differences from equal temperament are more evident to the pianist playing in it than to the listener. The best major thirds are grouped in the circle of fifths around C-E, whereas the perfect fifths become more perfect in the black keys, which all have fifths of 702 cents. This gives the keys related to C a sweet, gentle quality, the black-note keys an austere, noble quality, and middle keys like Eb and A a neutral, ambiguous quality."
| pure 5ths tuning (each 5th up, multiply by 3/2 & normalise; each 5th down multiply by 2/3 & normalise) |
| note name: | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | D# |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 371.250 | 278.438 | 417.656 | 626.484 |
| with pure 5ths, high D# is sharp to low Eb (for enharmonic equivalence, the ratio of frequencies must be that of a pure octave, i.e. 2:1) |
| Vallotti temperament in key of C: the Pythagorean comma is spread equally through 6 conjoined 5ths, F-C, C-G, G-A, D-A, A-E and E-B, each of which is narrowed by 1/6 of the comma, the remaining 5ths are pure |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 311.830 | 467.746 | 350.809 | 262.513 | 392.882 | 293.997 | 440.000 | 329.256 | 492.769 | 369.577 | 277.183 | 415.774 | 623.660 |
| from which calculation, the required Vallotti temperament scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 262.513 | 277.183 | 293.997 | 311.830 | 329.256 | 350.809 | 369.577 | 392.882 | 415.774 | 440.000 | 467.746 | 492.769 |
| Young temperament in key of C: the Pythagorean comma is spread equally through 6 conjoined 5ths, C-G, G-A, D-A, A-E, E-B and B-F# each of which is narrowed by 1/6 of the comma, the remaining 5ths are pure |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 311.127 | 466.690 | 350.018 | 262.513 | 392.882 | 293.997 | 440.000 | 329.256 | 492.769 | 368.743 | 276.557 | 414.836 | 622.254 |
| from which calculation, the required Young temperament scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 262.513 | 276.557 | 293.997 | 311.127 | 329.256 | 350.018 | 368.743 | 392.882 | 414.836 | 440.000 | 466.690 | 492.769 |
|
| 10 |
Italian eighteenth century
One of the many variations commonly in use in the eighteenth century that emphasized a pure third at C-E and distributed the "wolf" around the circle of fifths. There is only one pure interval in this scale.
| pure 5ths tuning (each 5th up, multiply by 3/2 & normalise; each 5th down multiply by 2/3 & normalise) |
| note name: | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | D# |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 371.250 | 278.438 | 417.656 | 626.484 |
| with pure 5ths, high D# is sharp to low Eb (for enharmonic equivalence, the ratio of frequencies must be that of a pure octave, i.e. 2:1) |
| Italian 18th C. temperament in key of C: the 5ths, Eb-Bb, Bb-F and F-C are widened by 1/12 of the comma; the 5ths, C-G, G-D, D-A and A-E are narrowed by 1/4 of the comma; the 5ths, E-B, B-F#, F#-C# and C#-G# are narrowed by 1/12 of the comma, while the 5th G#-D# is widened by 1/12 |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 311.127 | 467.218 | 350.809 | 263.404 | 393.770 | 294.329 | 440.000 | 328.884 | 492.769 | 369.160 | 276.557 | 414.368 | 622.254 |
| from which calculation, the required Italian 18th C. temperament scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 263.404 | 276.557 | 294.329 | 311.127 | 328.884 | 350.809 | 369.160 | 393.770 | 414.368 | 440.000 | 467.218 | 492.769 |
|
| 11 |
Temperament Ordinaire
In the near keys, the thirds are much purer and the fifths less so than in the remote keys. In the near keys, irregular temperaments resemble meantone, and in the remote keys, they resemble (the near keys of) Pythagoras' tuning (with the tense thirds). This gives added variety to modulation, which was appreciated in the past. Bradley Lehman, writing to Meantone, on the www.bach-cantatas.com website, argues that temperament ordinaire is more a process (or a strategy) than any specific outcome.
|
One starts from a regular meantone (whether 1/4, 1/5, or 1/6 comma) and then raises the sharps somewhat and/or lowers the flats somewhat (to taste) so more of the tonalities can be used in music. This is done usually by the simple expedient of tuning one or more pure fifths (instead of the normally tempered fifths of the regular meantone) during this fudging process. Sometimes, some of the resulting fifths even end up a bit wide - tempered in the "wrong" direction - for the greater goal of better playability in more keys. The strategy, all around, is to get the circle to meet itself relatively closely somewhere in the extreme sharps and flats, such that the notes can be used (albeit roughly) for one another. For example, playing an E-flat where the music says D#. In regular meantone, only one of those two would be available on the keyboard. In temperament ordinaire such pairs of notes become roughly interchangeable, although still not identical.
|
Reference:
|
| 12 |
Equal Temperament (ET)
This scale is so common in the twentieth century that many musicians and instrument makers tend not to know that there are alternatives.
Dividing the Pythagorean comma equally around the circle of fifths is not a recent idea.
One of the earliest mentions of equal temperament was by the Dutch mathematician Simon Stevin. He published his proposal for equal tempering as early as 1584.
A. D. Fokker, in Simon Stevin's views on music, writes that:
[i]t is Stevin's outstanding achievement that he produced the exact proportional numbers, between 10000 and 5000, in four figures, representing the steps of twelve semitones in the octave leading from 1 to 1/2. He was able to do so, referring to his French work on arithmetic ... where he had shown that the requirement of twelve equal ratios leading from 2 to 1 involves the twelfth root of 2. By combining the operations of computing two square roots and subsequently a cube root, he finds for the twelfth root of 2 the ratio 10000 : 9438 = 1.0595 : 1. The more exact figure is 1.059463 . . . . . Stevin never mentions the approximate value 18/17, familiar to makers of lutes, who used it in fixing frets on the fingerboards. |
It is from this source that we have it confirmed that while meantone tunings with pure or near-pure thirds were standard on keyboards, ET was standard on fretted instruments such as the lute. However, for a long time it was not considered satisfactory due to the impurity of all the intervals.
Many commentators have suggested that equal temperament (ET) on keyboard instruments is really a twentieth century idea and was not widely used before that.
Peter Bavington, writing on the clavichord mailing list makes the following comment:
According to Thomas McGeary (German-Austrian Keyboard Temperaments and Tuning Methods, 1770-1840: Evidence from Contemporary Sources in 'Journal of the American Musical Instrument Society' No. 15 (1989)), the tuning and maintenance manual published in 1805 by 'a certain Gall' reprints the entire section on tuning from Büttner and Nacherberg's Stimmbuch of 1801: this contains instructions for only one temperament, not very clearly explained but ET is certainly intended. Christian Thon's manual of 1817 refers to two possible methods of temperament, ET and quarter-comma mean-tone. McGeary shows that he is quite unique among German sources in referring to mean-tone at this late date. All other sources describe only ET or ET and Kirnberger II. One of the interesting things about McGeary's survey is that it shows the wide influence that Kirnberger had: several manuals refer to Kirnberger II as if it was the only alternative to ET. |
Fred Sturm comments on Daniel Gottlob Türk's 1789 Klavier Schule:
[Türk] describes ET as having "one key as pure as every other" and says that "the required deviation is so insignificant that our ears have become accustomed to it, and a keyboard tuned in this way can be considered as being in tune." He addresses the controversy surrounding the connection of "key colour" with unequal temperament, a controversy created mostly by Kirnberger and sustained by him and his followers. Türk's wording is rather careful, but if one reads between the lines, it is clear that, while trying not to antagonize the influential Kirnberger, he really doesn't buy the argument. As one example, he notes a composer (Graun) who had composed a well known piece in accordance with principles of key colour, and ironically wonders how it must have sounded since it was written before Kirnberger had set forth his temperament method. He wonders whether any violin has ever been tempered according to Kirnberger's principles. The context leaves it crystal clear to me (the commentator, Sturm) that he didn't buy Kirnberger's arguments at all, and was very slyly and indirectly poking fun at him.
He notes Kirnberger's argument that ET is impossible (how can one temper all fifths by 1/12 Pythagorean comma with accuracy), and wonders whether it is possible to tune nine successive just fifths any more precisely (as in Kirnberger's scheme). But "I do not wish to declare myself here in favour of one temperament or the other..." However, he states that "Kirnberger finds the hitherto almost generally accepted equal temperament not useful enough. Taken in total, I (Sturm) find in Türk's writing rather strong evidence for the notion that ET was quite well established in the second half of the 18th century in Germany, which is in line with the bulk of the evidence. |
In the late 18th- and 19th- centuries, composers began increasingly to explored modulation to more distant keys. They found that most temperaments were unsatisfactory because of the significant tonal changes involved in changing keys. The equal-tempered scale was begrudgingly recognized as an acceptable compromise that worked equally well in every key. It is only through over a century of dominance that this scale has become the one that we are accustomed to - the scale that sounds "in tune" to us today. It is actually one type of 'meantone' tuning because the third lies exactly midway between the root and the fifth.
| pure 5ths tuning (each 5th up, multiply by 3/2 & normalise; each 5th down multiply by 2/3 & normalise) |
| note name: | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | D# |
| frequency (Hz) | 309.026 | 463.539 | 347.654 | 260.741 | 391.111 | 293.333 | 440.000 | 330.000 | 495.000 | 371.250 | 278.438 | 417.656 | 626.484 |
| with pure 5ths, high D# is sharp to low Eb (for enharmonic equivalence, the ratio of frequencies must be that of a pure octave, i.e. 2:1) |
| Equal temperament in key of C: all the 5ths are narrowed by 1/12 of the Pythagorean comma |
| | Eb | Bb | F | C | G | D | A | E | B | F# | C# | G# | Eb |
| frequency (Hz) | 311.127 | 466.164 | 349.228 | 261.626 | 391.995 | 293.665 | 440.000 | 329.628 | 493.883 | 369.994 | 277.183 | 415.305 | 622.254 |
| from which calculation, the required equal temperament scale can now be constructed |
| scale notes: | on C | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| frequency (Hz) | | 261.626 | 277.183 | 293.665 | 311.127 | 329.628 | 349.228 | 369.994 | 391.995 | 415.305 | 440.000 | 466.164 | 493.883 |
|
|
|
Temperament/Tuning and Pitch Calculator
::

|
Key words:
temperament
tuning
calculator |
| 1 |
Temperament/Tuning and Pitch Calculator
For understanding how to use beat tables see the section below entitled beats and tuning.
Note : Temperament Unit (TU) notation, developed by the organ builder John Brombaugh, is a system for describing very small intervals as integer values. It is a logarithmic system similar to that of 'cents', but designed to be easier to understand and use than cents notation when working with divisions of the commas. A TU is defined as 1/720th of the interval of a ditonic or Pythagorean comma. That is, -720 TU must be distributed among the twelve fifths in a "circle of fifths" to remove the excess over seven octaves. One major benefit of this system is that the other important comma (syntonic comma) works out to be almost exactly 660 TU, and the difference between the two commas (the 'schisma') is therefore 60. All three of the numbers 720, 660, and 60 are easily divisible by 1, 2, 3, 4, 5, 6, and 12, the divisors used in describing most temperaments. Therefore, most temperaments can be described in TUs using only integer values, without the use of a calculator. There are approximately 36829 Temperament Units in an octave.
Temperament calculators can never 'tell' you which temperament you must use when playing a particular piece of music. Indeed, one can rarely be sure even which temperament the composer had in mind as he put pen to paper. Circumstantial evidence (for example: the key chosen, the progressions used (and particularly the progressions avoided) and the keys to which the piece might modulate) may often eliminate certain choices of temperament but one needs to seek evidence elsewhere than our calculator when deciding which set up is most appropriate. The purpose of this resource is to bring the suggestions of musical theorists and musicians to one place and, with the beat table above, make it possible for anyone with a modest degree of skill to set up accurately a particular temperament on their own instrument. In our opinion, temperaments can only make sense when they are heard.
|
| 2 |
Source References for Data on Temperaments
12T: (12-Tone Scale Tuning Temperaments) - http://www.microtonal-synthesis.com/GS_XG.html
Andrew Purdam: http://members.tip.net.au/~apurdam/tempers.html
Kyle Gann: http://www.kylegann.com/histune.html
Joe Monzo: http://tonalsoft.com/enc/encyclopedia-index.aspx
IT: (Temperaments for Instrument-Tuner) - http://www.instrument-tuner.com/temperaments.html
TB: Terry Blackburn: Alternate Temperaments: Theory and Philosophy - http://www.terryblackburn.us/music/temperament/index.html
EF: Tuning, temperaments and the traverso - http://www.earlyflute.com/pages/traversotuning.htm
DH: David Hitchin (private communication) - David's data includes references to published work by:
- B = J. Murray Barbour, Tuning and Temperament: A historical survey. 1951, reprinted by Dover Publications 2004
- D = Thomas Donahue, A guide to musical temperament. Scarecrow Press, 2005
- E = Early Music, August 2005, letters
- L = Bradley Lehman, e&c, www.larips.com; Temperament Calculator. www.how.to/tune
- N = Johan Norrback, A Passable and Good Temperament. Göteborg University, 2002
- Pa = C. A. Pagham, The Well-Tempered Organ, Positif Press, 1995
- Po = Paul Poletti, Temperaments for Dummies, www.polettipiano.com/Media/T4D.PDF
WD = William Drake, William Drake Organs - information about 'Grosvenor' and 'Hamburg' temperaments
Sc: Scala project scale library: more information at Scala
W: Wikipedia: Werckmeister temperament
GB: Temperaments by Groenwald, Berlin
Other References:
Christopher Stembridge, "Music for the Cimbalo Cromatico and other Split-Keyed Instruments in Seventeenth-Century Italy," Performance Practice Review 5.1 (Spring, 1992), published by the Claremont Graduate (ISSN 1044-1638)
Scala
Virtual Silbermann Organ
Wintemper - the versatile & free multi-temperament tuner for Windows
Chromatia - chromatic multi-temperament instrument tuner
The UNEQUAL TEMPERAMENTS free downloads and other goodies made available by Claudio Di Veroli.
- Scala is a powerful software tool for experimentation with musical tunings, such as just intonation scales, equal and historical temperaments, microtonal and macrotonal scales, and non-Western scales. It supports scale creation, editing, comparison, analysis, storage, tuning of electronic instruments, and MIDI file generation and tuning conversion. All this is integrated into a single application with a wide variety of mathematical routines and scale creation methods. Scala is ideal for the exploration of tunings and becoming familiar with the concepts involved. In addition, a very large library of scales is freely available for Scala and can be used for analysis or music creation.
Fred Nachbaur's MIDI tempering utilities
|
|
|
Beats and Tuning
::

|
Key word:
beats |
| 1 |
Beats and Tuning
We would refer our readers to the excellent article The Equal Tempered Scale and Some Peculiarities of Piano Tuning by Jim Campbell which explains what beats are and how they are used to set tunings and temperaments. Another excellent resource that we would recommend is the High School Physics Tutorial entitled Behavior of Sound Waves which includes some nice diagrams to aid understanding.
We quote almost verbatim from the comprehensive article on piano tuning that is to be found on Wikipedia. The method described can be applied also to the tuning of clavichords, harpsichords, organs, harps, and so on.
|
The relationship between two pitches, called an interval, is the ratio of their absolute frequencies. Two different intervals are perceived to be the same when the pairs of pitches involved share the same frequency ratio. The easiest intervals to identify, and the easiest intervals to tune, are those that are just which have a simple whole-number ratio. The term temperament refers to a tuning system which tempers the just intervals (usually the perfect fifth which has the ratio 3:2) in order to satisfy some other mathematical property; in equal temperament, to temper a fifth one slightly narrows it by flattening its upper pitch slightly, or raising its lower pitch slightly. A system of temperament can also be known as a set of bearings, a term derived from early treatises on temperament which asserted that a fifth could be flattened "as much as it can bear".
Tempering an interval produces a beating, which is a fluctuation of the intensity of sound heard when an interval is played. It should be noted that the use of 'beats' to check the tempering of intervals does not appear in historical tuning methods until after the end of the seventeenth century. Because the actual note from a vibrating string is not one pitch but a complex of pitches arranged in a harmonic series, the rate of beating is determined by the difference between the frequencies of any harmonics that coincide (for a fifth this would be the third harmonic of the lower note and the second harmonic of the upper note; for a major third this would be between the fifth harmonic of the lower note and the fourthth harmonic of the upper note). The beats are heard clearly when these two pitches are close enough together that this difference is small (less than 20 hertz (Hz)). Where these frequencies can be calculated, a temperament may be tuned aurally by timing the beat rates.
One practical method of tuning the piano begins with tuning a set of strings in the middle range of the piano to a temperament octave. Once these strings are tuned, the tuner may proceed to tune all other pitches by comparing octave intervals against this temperament octave. This is convenient, because the octave is the most easy interval to tune (having the simplest ratio of 2:1) after the unison (1:1). (These octaves are tuned to have no beating.)
|
The use of 'beat rates' to aid tuning is well documented.
The English author Roger North (c.1726) writes:
|
"... one may observe, as I have done sitting by an operator at work, that in tuning 2 pipes to an octave there shall be first (when wholly discordant) an intollerable jarr, and as the artist moves the plugg or plate to reduce the sound to a consonance, first it shall come to a distinguisht beating very swift and chattering, and so slower, and at length to a sort of wallowing of the sound, and at last fall into the consonance, as into a notch, and there flow with all the quiet eveness imaginable ... those artists judge of tuning ... not by the sweetness or unity of sound, but by the not striving, beating, shaking or wallowing ..."
"... this [hint] is to help a learner to find out the way to come at the accord he aimes at; but the justice of it, according to the purest harmony, is more nice, and requires another sort of observation; and that is of the chattering, wallowing, or rowling of two notes sounding together, which will be very notable. till the accord is exact ..."
"... [when setting a temperament] some observe the beats or wallows of the sound, and leave them to goe on in time as slow quavers ..."
|
Reference:
- John Wilson (ed.) Roger North on Music, Novello (1959)
The calculator above lists the beat frequencies between notes for particular temperaments or tunings. It also displays the absolute frequencies of the different scale notes; it is assumed that a' is set with a tuner or a fork (which choice establishes the overall pitch of the scale).
For equal temperament, begin by tuning one note to the other so that the beating disappears, temper that interval in the appropriate direction, either making the interval wider - the pitches to be further apart than if they were justly tuned, and the beat rate shown positive - or narrower - the pitches to be closer together than if they were justly tuned, and the beat rate shown negative, until the desired beat rate is achieved.
The beat rates assume the given note (at the top of the column) has already been set and the tuner is now setting the chosen interval (see left hand column) above the given set note: thus, for a Pythagorean tuning using a chain of fifths, all fifths are pure (beat rate = 0) except the one between G# and D# (a fifth above) which interval has to be narrowed to eliminate the Pythagorean comma (row perfect 5th: G# to fifth above - beat rate -16.86: D# is flattened).
If one is tempering to a Vallotti temperament for a'=415Hz then the beat frequency for the major third f to a (in the tenor octave) is to be found at the intersection of the column headed 'f' and the row headed '5-limit major 3rd (5:4)'. The beat frequency is 2.81Hz. For a'=440Hz, the beat frequency for the same interval would be 2.98Hz. The beat frequencies are rounded to two decimal places.
Slower beat rates can be carefully timed with a metronome, or other such device. For the thirds in the temperament octave, it is difficult to tune so many beats per second, but after setting the temperament and duplicating it one octave below, all of these beat frequencies are present at half the indicated rate in this lower octave, which are excellent for verification that the temperament is correct.
One of the easiest tests of equal temperament is to play a succession of major thirds, each one a semitone higher than the last. If equal temperament has been achieved, the beat rate of these thirds should increase evenly over the range of the keyboard instrument.
|
|
|
Information on Temperaments
::

|
Key word:
beats |
| 1 |
Information on Temperaments
Books:
- History of Musical Acoustics by S. Donval, Fuzeau Publishing, France
- Temperament by Stuart Isacoff published Faber and Faber (originally by Alfred Knopf)
- Tuning and Temperament by J. Murray Barbour published Michigan State College Press
- Fundamentals of Musical Acoustics by Arthur H. Benade published Dover Publications
- The Structure of Recognizable Diatonic Tunings by Easley Blackwood published Princeton University Press
- Treatise on Harpsichord Tuning by Jean Denis published Cambridge University Press
- Tuning: Containing the Perfection of Eighteenth-Century Temperament, the Lost Art of Nineteenth-Century Temperament and the Science of Equal Temperament by Owen H. Jorgensen published Michigan State University Press
- Lutes, Viols and Temperaments by Mark Lindley published Cambridge University Press
- Intervals, Scales and Temperaments by Lt. S. Lloyd and Hugh Boyle published MacDonald, London
- Musical Temperaments by Erich Neuwirth published Springer Verlag
- Musicalische Temperatur by Andreas Werckmeister published Diapason Press
- A guide to musical temperament by Thomas Donahue published Scarecrow Press, 2005 (recommended by David Hitchin)
- How equal temperament ruined harmony (and why you should care) by Ross W. Duffin, Norton, 2007 (recommended by David Hitchin)
- German-Austrian Keyboard Temperaments and Tuning Methods, 1770-1840: Evidence from Contemporary Sources by Thomas McGeary: Journal of
the American Musical Instrument Society No. 15 (1989)
- Schubert: The Piano and Dark Keys by Elizabeth Norman MaKay (ISBN 978 3 7952 1289 6)
Online
A useful link to a spreadsheet for the calculation of fret placement on lutes and viols, based on a number of historical temperament systems,
may be found on the "Downloads" page of the Lute Society of America website, Lute Society of America.
|
|
|
Timbre/Tone Colour
::

|
Key words:
timbre
tone colour |
| 1 |
Timbre/Tone Colour
All musical instrument have acoustical properties determined by their form and material of construction. Musical instruments require intervention from an actuator (or performer) to provide the energy that will initiate the production of sound. Sound is a form of mechanical energy that requires a medium through which to propagate or travel. A sound travels from a source, through a medium to a detector. For us the detector is the human ear. If the sound is to be considered musical with a specific pitch or tone quality, rather than just 'noise', the mechanical energy has to radiate from the instrument as regular disturbances, what we call 'periodic' vibrations. The vibrator producing fluctuations, oscillations, pulsations or undulations (these terms are all equivalent) will be different on different instruments and the initiation and resonance may arise from two separate processes. We say that the sound producing system has two parts - the initiator and the resonator. Examples of initiators: - String - violin, guitar, piano, psaltry, harp
- Reed - clarinet, oboe, bassoon, English horn.
- Lips - trumpet, trombone, French horn, tuba.
- Membrane - drum, tambourine
- Wood - wood block, xylophone.
- Metal - bells, cymbals.
- Electronic instruments - speakers that can produce vibrations
Examples of resonators: - Wooden box which may be hollow or solid - violin, guitar, piano (sounding board)
- Tubing - (brass, silver, wood, pipe-like) - trumpet, trombone, French, horn, flugel horn, tuba, trombone.
- Chest, oral, nasal and throat cavities - human voice.
- Electronic instruments - amplifier, tuned circuits.
The character of the sound each instrument produces is, therefore, partly due to vibrations associated with the process of initiation and partly due to the characteristic vibrations that are generated by the resonator, initially sustained but usually decaying once energy is no longer supplied to the system. If, on a stringed instrument, the bow is continuously drawn across a string, the instrument is described as being in continuous-control mode; i.e. onset - sustain. If, however, on the same instrument, a string is plucked with a finger, the instrument is then said to be in envelope-based mode; i.e. onset - sustain - decay. In general and when the process of initiation is mechanical and occurs over a relatively short time, short relative to the persistance of the resonance response that follows, a note has a clear starting or 'onset' sound (arising from the initiator) which is distinguishable from the sound that follows (that arising from the resonator). For example, the 'tonguing' sound that begins notes produced on wind-instruments is distinguishable from the sustained resonance associated with the remainder of the note. The percussive initiation of a note produced on a piano, the sound of the hammer striking the string, is distinguishable from the sound that rings on should you keep the piano key depressed for any length of time. The mechanical processes involved in sound production on musical instruments include plucking or bowing (on violin, viola, cello string bass, harpsichord), blowing (on clarinet, oboe, trumpet, trombone, recorder, voice) or striking (on drums, piano, clavichord, xylophone). It has been found that if the onset is removed from recordings of sounding musical instruments it becomes more difficult to distinguish one from another. External factors, too, can influence 'timbre' - for example, if an instrument moves in a room relative to the listener. To summarise, timbre is the spectrotemporal pattern of a generated sound indicating the way the energy in the system is distributed between different harmonics or frequency components and the way that distribution is changing over time. The instruments of the orchestra, viewed as mechanical systems, can be classified in the following manner:
- Strings
- Bowed: Violin, viola, cello, double bass, bowed psaltry
- Plucked: Violin, viola, cello, double bass, lute, harp, citern, sitar, shamisen, mandolin, harpsichord
- Hammered: Zither, dulcimer, plucked psaltry
- Struck: Piano, clavichord
- Woodwinds
- Blown Flute: Transverse flute, recorder
- Blown Single reeds: Clarinet, bass clarinet, saxophone
- Blown Double reeds: Oboe, bassoon, contra bassoon, crumhorn
- Brass
- Blown: Cornet, trumpet, French horn, trombone, Flugel horn, tuba
-
Percussion
- Struck Tuned
- Bells, chimes
- Glockenspiel
- Xylophone, vibraphone, marimba
- Timpani
- Struck Untuned
- Bass and snare drums
- Cymbals
- Tam-tam
- Gong
- Claves, maracas, bongos, tambourine, whip, triangle, woodblock, bells
Reference:
Examine Timbre
|
|
|
Classification of Common Musical Instruments
::

|
Key words:
timbre
tone colour |
| 1 |
Classification of Common Musical Instruments
Aerophones
(Wind Instruments - Vibrating Air) | Chordophones
(Stringed Instruments - Vibrating Strings) | Idiophones
(Vibrating Instruments) | Membranophones
(Vibrating Membrane Instruments) | Electrophones
(Electronically Created Sounds) | | Free Aerophones | Free Aerophones
(Moving object vibrates air to create sound) | | | | Bull-roarer
Buzzer | Free Reed Aerophones
(Vibrating reeds without resonators) | | | | Accordion
Harmonica
Harmonium
Mouth Organ
Sheng |
| Flutes (Flue Voiced)
(Air column split by lip of of the instrument) | | Open Tube | | | End Blown Single Flutes | | | | Kaval | | | End Blown Multiple Flutes | | | | Panpipes
Antara | | | Whistle Blown | | | | Boatswains Whistle
Flageolet
Recorder
| | | Side Blown | | | | Flute (transverse) | | Closed Tube | | | | Ocarina | | Keyboard | | | | Organ |
| Reedpipes
(Vibration of reeds) | Double Pipes
Triple Pipes
Hornpipes
Bladder pipe | | | | Crumhorn | | Bagpipes | | | | Musette | | Shawm | | | | Oboe
Cor Anglais or English Horn | | Rackett | | | | Sordone
Sordun | Bassanelli
Bassoon | | | | Curtal
Bassoon
Contrabassoon
High-pitched Bassoon
Single-reed Bassoon | Sarrusophone
Single-reed Reedpipes | | | | Clarinet
Saxophone | | Free-reed Aerophones |
| Lip Vibrated Aerophones
(Vibration of Lips) | Horn
Fingerhole Horns | | | | Cornett
Serpent | | Trumpet | | | Conical Bore | | | | Alphorn
Bugle
Cornet
Euphonium
Flugelhorn
Tuba | | | Cylindrical Bore | | | | English Baritone Horn
Sousaphone
Trombone |
| | Zithers | Ground Zithers
Musical Bows | | | Aeolian Bows
Pluriare | | Stick Zithers | | | Vinã
Bladder and String | Raft Zither
Trough Zither
Frame Zither
Tube Zither
Board Zither
Long Zither | | | Individually Bridged Long Zither
Fretted Long Zither | | Box Zither | | | Monochord
String Drum
Trumpet Marine
Psaltery
Aeolian Harp
Fretted Zither
Bell Harp | | | | Autoharp
Dulcimer
Zither |
| | Keyboard Chordophones | | Keyboard | | | Experimental Keyboard
Transposing Keyboard | Chekker
Dulce Melos
Clavichord | | | Cimbal d'amour | | Harpsichord | | | Clavicytherium
Gut-strung Harpsichords &
Enharmonic Harpsichords
Spinet
Virginal
Claviorganum
Piano-organ | | Bowed Keyboard Instruments | | Pianoforte | | | Harpsichord Piano
Tangent Piano
Sustaining Piano
Pedalboard Piano
Enharmonic Piano
Player Piano
Fortepiano
Piano |
| | Lyres | | | Lyre
Crwth |
| | Harps | Ground Bows
Harps | | | Harp | Harp Zither
Harp Lute |
| | Lutes | Long-necked Lute
Short-necked Lute
Archlute | | | Theorbo
Theorbo Lute
Chitarrone
Angelica | Mandora
Mandolin
Sitar
Cittern | | | Archcittern | | Bandora | | | Orpharion
Penorcon
Polyphant
Balalaika
Charango
Colascione | | Guitar | | | Gittern
Vihuela
Spanish Guitar
Bass Guitar
Bandurria
Ukulele | Organistrum
(hurdy-gurdy) |
| | Bowed Chordophones | Bow
Fiddle
Rebec | | | Kit
Folk Rebec
Polnische Geige | | Lira da Braccio | | | Lira da Gamba | Viola da Gamba
Violone
Baryton
Viola | | | Violino d'amore | | Violin | | | Viola
Tenor Violin
Violoncello or 'Cello
Double Bass |
| | Concussion Idiophones | | Clappers | | | Claves
Slapstick | Castanets
Cymbals |
| | Percussion Idiophones | Stamped Idiophones
Percussion Beams | | | Marimba
Bell Lyre
Celesta
Gender
Glockenspiel
Orchestra Bells
Saron
Vibraphone | | Percussion Disks | | | Gong | | Percussion Sticks | | | Triangles | | | Xylophone | | | | Crystallophones
Lithophones
Metallophones | | Percussion Tubes | | | Stamping Tubes
Slit Drums
Tubular Bells & Chimes
Angklung | | Percussion Vessels | | | Percussion Gourds & Pots
The Echeion
Steel Drums
Bells | | | | Temple Blocks
Wood Block |
| Shaken Idiophones
(Rattles) | | Vessel Rattles | | | Pellet Bells | | | Gourd Rattles | | | | Maracas | | | Basketry Rattles
Hollow Ring Rattles | | Suspension Rattles | | | Stick Rattles
Sistrum
Strung Rattles | | Frame, Pendant, and Sliding Rattles | | | Sistro |
| | Scraped Idiophones | | Scrapers | | | Güiro | | Cog Rattles | | | Cog Rattle
Ratchet
Washboard
|
| | Split Idiophone |
| | Plucked Idiophones | | | Jew's Harp | | Thumb Piano | | | Music Box
Sansa
Mbira |
| | Friction Idiophones | Friction Sticks
Friction-bar Pianos
Friction Vessels | | | Musical Glasses
Glass Armonica
Musical Saw |
| | Predrum Membranophones | Ground drums
Pot drums |
| | Tubular Drums | Frame Drums
Shallow Drums
Cylinder Drums
Hourglass Drums
Conical Drums
Goblet Drums
Barrel Drums
Rattle Drums
Water Drums
Drum Kit / Drum Set
Talking Drums
Drum Chimes | | | Bass Drum
Bongos
Conga
Snare Drum
Tenor Drum
Timbales
Tom-tom |
| | Kettledrums | | | Timpani |
| | Friction Drums |
| | Mirliton | | | Kazoo |
| | Synthesizers | | | Moog
Theremin
Ondes Martenot
Trautonium | |
References:
List of musical instruments by Hornbostel-Sachs number
Taxonomy of Musical Instruments by Henry Doktorski
|
|
 :: next lesson :: next lesson
| |
 :: next lesson
:: next lesson

