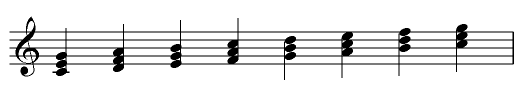|
Concord & Discord
::

|
Key words:
music
noise
concordant
discordant
consonance
dissonance
form
function |
| 1 |
Concord & Discord
The distinction between what we would call music and what we would regard as noise is a matter of personal taste. We might use words like concordant and discordant to distinguish the acceptable from the unacceptable. Musical theorists discussing harmony have a particular technical use for the words concord as applied to chords or consonance as applied to intervals, as well as to discord as applied to chords or dissonance as applied to intervals.
Most cultures employ 'tunes' or 'melodies' in their music but Western music is particularly distinctive through its use of 'harmony' whether arising from the interweaving of other musical lines around and about a 'melody line' (what we call 'counterpoint') or through the support of a 'melody line' with a progression of 'chords', groups of notes sounding simultaneously, groups made up of various musical intervals.
Todd McComb explains:
The use of chords, or what we might call "vertical structure" to distinguish it from the "horizontal structure" defined principally by melody, is a topic which is both crucial for understanding [medieval] music itself and illustrative of general conclusions about polyphonic music. First it is important to understand that medieval composers did not use "harmony" in a sense which classical composers would have understood. This is perhaps most easily grasped by realizing that the lowest voice of many of the most elaborate polyphonic works of the period consists of a pre-existing melody, often plainchant. Other melodies were added to these, and each layer would have its own horizontal concerns. Of course, in the greatest masterpieces, the vertical elements add something tangible to this mix, without sacrificing the horizontal beauty.
[In medieval music, c]adential motion, i.e. the way in which individual phrases are brought to a close, is crucial for understanding this structure... Such ending motion is crucial to horizontal ideas as well, just as the "final" (or last note) of a mode is fundamental to defining it. Of course modality is a theoretical idea specifically developed for application to the system of Gregorian plainchant which underlies medieval polyphony, and so is never too far removed from polyphonic music. Nonetheless, it is generally not possible to assign modality to polyphonic music of this period, unless it is notionally assigned based on that of the lowest voice, a common technique.
|
Reference:
We might say that some harmonic intervals have a 'sweeter' sound than others; we call them consonances. The perfect consonances are the unison (although many theorists do not include the unison in their list of intervals), the 5th and the octave. The imperfect consonances are the major 3rd, minor 3rd and their respective inverses, the minor 6th and major 6th. The 2nds and 7ths, both major and minor, are dissonances. One, the augmented 4th, has its own name, the tritone (meaning 'three tones'; the interval is six semitones wide - e.g. c to f#). Medieval theorists considered this interval so unpleasant that it was strictly forbidden and known as the diabolus in musica.
At this point we should draw attention to what Rene Descartes (1596-1650), the French philosopher, writing on the 4th March 1630 to his friend Marin Mersenne (1588-1648), has to say about 'sweetness' in music:
"... it is one thing to say that one consonance is sweeter than another, another thing to say it is more pleasing. Everyone knows that honey is sweeter than olives, yet many would prefer to eat olives, not honey. Thus, everyone knows that the fifth is sweeter than the fourth, the fourth sweeter than the major third, this in turn sweeter than the minor third. Yet there are places in which the minor third is more pleasing than the fifth; others indeed, where a dissonance is more pleasing than a consonance." |
Today, aware of the psychological dimension in the perception of sound and harmony, we might distinguish between two types of consonance. In the first case, our approach would be purely functional, according to the 'rules' of music theory, where a major third is a consonant interval regardless of other concerns. This sort of consonance we might term musical consonance. The second approach, which depends on the pitch of the notes involved and their timbre, might lead us to argue that a major third might be relatively more or less psychologically consonant. Thus, psychological consonance is centred on a sensory approach to the perception of sound, while musical consonance sees sound purely as a mathematical construct.
We have already mentioned how the 'leading note' in a major scale 'pulls' the melodic line towards the tonic, one semitone higher. Chords too, give a sense of movement to a piece of music. When all the intervals are consonances, the chord feels stable and is a concord. Chords with dissonances, that call out to be 'resolved' (requiring that certain notes move up or down), are discords.
We must appreciate that intervals and chords have both form (what they are, how they are 'built') and function (whether they are 'stable' or 'unstable', where they are leading).
The intervals perfect fourth, augmented fourth and diminished fifth are ambiguous as to whether they are consonant or dissonant. Where one note of any of these intervals lies as the bass of a chord, the interval is dissonant. However, if both notes form upper constituent notes of a chord, they are consonant. In this case function overrules form. We will consider these matters further when discussing progressions.
Reference:
|
|
|
Triads
::

|
Key word:
triad
Roman numerals
primary triad
secondary triad
major triad
minor triad
augmented triad
diminished triad
close position
open position |
| 1 |
Triads
We examined intervals in an earlier lesson. Intervals are always made up of two notes. We now want to discuss 'chords' and, particularly, chords made up of three notes chosen in a particular way. These 'chords' are called triads. The triad is made up of the root, which is the lowest note in the chord, together with the 3rd and 5th above it. If the root is one of the degrees of a major or minor scale then the triads are given Roman numerals or names identifying that degree, in the following way: I (tonic triad), II (supertonic triad), III (mediant triad), IV (subdominant triad), V (dominant triad), VI (submediant triad), VII (leading note triad) The tonic (I), subdominant (IV) and dominant (V) triads are called primary, the remainder (except that on VII) are called secondary. The triad on VII is diminished and is a discord (although its first inversion is not) 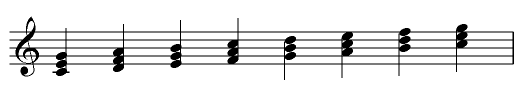 In addition, the triads are classified according to the quality of the 3rd or 5th; i.e. whether diminished (for 3rd or 5th), major (for 3rd), minor (for 3rd) or augmented (for 3rd or 5th).
| triad quality | how marked | how constructed (I) | how constructed (II) |
| major triad | unmarked or marked 'ma', with upper case Roman numerals
(upper case because the 3rd is major) | a major 3rd
with
a perfect 5th | a minor 3rd
above
a major 3rd |
| minor triad | marked 'mi' or numbered with lower case Roman numerals
(lower case because the 3rd is minor) | a minor 3rd
with
a perfect 5th | a major 3rd
above
a minor 3rd |
| augmented triad | marked + or 'aug', with upper case Roman numerals
(upper case because the 3rd is major) | a major 3rd
with
an augmented 5th | a major 3rd
above
a major 3rd |
| diminished triad | marked ° or 'dim', with lower case Roman numerals
(lower case because the 3rd is minor) | minor 3rd
with
a diminished 5th | a minor 3rd
above
a minor 3rd |
The notes in a triad can be arranged so that the root is no longer the lowest note of the three. If the 3rd is the lowest note, the triad is said to be a 'first inversion' (using Roman notation, denoted by an additional 'b'; e.g. Vb) and when the 5th is the lowest note, the triad is said to be a 'second inversion' (using Roman notation, denoted by an additional c; e.g. Vc). For completeness, the root position may be denoted by an additional 'a'; e.g. Va. Triads where all the notes lie in positions closest to the other notes in the chord, are said to be in 'close' position, otherwise the triads are said to be in 'open' position. Let us now summarise the triad harmonisation of the major and minor scales using numbered chords: 
We thank Cedric Debono for helping us correct two misprints in an earlier version of this page.
Notice the 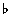 sign in front of III, VI and VII in the natural minor scale. All minor scales are named 'relative' to the major scale on the same key-note. The use of accidental signs in front of numbered chords should be understood to refer to 'raising' or 'lowering' notes in the chord and not necessarily the use of a 'sharp' or 'flat' sign to achieve this. So a 'sharpened' B flat becomes B natural, i.e. 'raised' or 'sharpened' by a semitone. sign in front of III, VI and VII in the natural minor scale. All minor scales are named 'relative' to the major scale on the same key-note. The use of accidental signs in front of numbered chords should be understood to refer to 'raising' or 'lowering' notes in the chord and not necessarily the use of a 'sharp' or 'flat' sign to achieve this. So a 'sharpened' B flat becomes B natural, i.e. 'raised' or 'sharpened' by a semitone.
There is one further important point that should be noted. In the major, harmonic minor and melodic minor scales above the triad on the dominants are major (the third is a B natural). The B natural is the leading note to the tonic C and this is the most important factor in the dominant fifth wanting to move to a triad or chord of the tonic. In the natural minor, the dominant triad is minor (the third is a B flat) and the pull to the tonic is much weaker. Only when the third is a major third is the triad on the fifth a dominant triad.
Let us finish by listening to some of these triads.  To hear them press the play button displayed below.
|
|
|
Diatonic Triads
::

|
Key word:
diatonic triad |
| 1 |
Diatonic Triads
One question that has been asked about triads is 'what is the strict meaning of diatonic triad?' When, earlier, we discussed the difference between chromatic and diatonic notes we pointed out that notes in the major and minor scales of a particular key note are diatonic while those that do not appear in these scales are 'chromatic' (see lesson 11 - The Diatonic Scale). So in the key of C, E natural (which appears in the C major scale) and E flat (which appears in the C minor scale) are diatonic but E sharp (which appears in none of the C scales) is chromatic. A triad is a chord with three notes and three intervals, i.e. if the notes are named X, Y and Z then the three intervals are (i) between X and Y, (ii) between X and Z and (iii) between Y and Z. When written in its close root position, this means that the lowest note is the root, the lowest and the middle notes are an interval of a third apart and the middle to the highest notes are an interval of a third apart. The interval between the lowest and the highest notes is a fifth. So, a triad, written in its close root position, is formed from two thirds placed within a fifth. The root functions as the key note when determining whether or not the other two notes in the triad are diatonic or chromatic and therefore whether the triad is diatonic or not. If the root is C and the triad is [C - E - G] or [C - E flat - G], then the triad is diatonic, because E, E flat and G all appear in scales on C. The triads [C - E - G sharp] and [C - E flat - G flat] are not diatonic because neither G sharp nor G flat appear in the major or minor scales on C.
|
|
|
Chords
::

|
Key words:
chords
seventh chord
dominant chord
discordant
consonance
dissonance
form
function |
| 1 |
Chords
Chords can exist in isolation but Western music uses them in progression. We need to understand how they relate to one another. This becomes increasingly important when our chords are made up of a larger number of notes. We need to distinguish 'close' and 'open' harmonies (as with triads), chords where notes are repeated at different pitches, and chords where 'extra' notes are included (i.e. 7th, 9th, etc.). As we increase the number of different notes we find that the same arrangement of notes can be 'named' in more than one way and there are also many more 'inversions' possible. Diatonic triads to which a seventh is added are called 'diatonic 7th' chords and are marked with the chord token 7. For example, V7a, from which the 'a' is usually omitted, i.e. V7, is a dominant 7th in root position while V7d is a dominant 7th, fourth inversion. The 3rd above the root of the dominant chord in minor keys (which is the 7th degree or leading note of the scale) is always raised a semitone.
Let us finish by summarising the harmonisation in sevenths of the major scale using numbered chords: Ima7 IImi7 (or ii7) IIImi7 (or iii7) IVma7 V7 VImi7 (or vi7) VIImi°(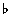 5) (or vii°( 5) (or vii°(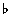 5)) 5)) where °, as we saw above, is shorthand for 'diminished'; and the harmonisation in sevenths of the natural minor scale using numbered chords: Imi7 (or i7) IImi7(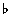 5) (or ii7( 5) (or ii7(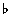 5)) 5)) 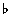 IIIma7 IVmi7 (or iv7) Vmi7 (or v7) IIIma7 IVmi7 (or iv7) Vmi7 (or v7) 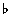 VIma7 VIma7 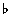 VII7 VII7 These points are examined in greater detail in lesson 17.
|
|
|
Chords in Jazz
::

|
Key words:
chords
jazz |
| 1 |
Chords in Jazz
Practical chord notation can be much simpler than that used by musical theorists because far fewer chord patterns are met with in real life than can be imagined by the fevered mind of an academic. In jazz, the root of the triad is named with a capital letter, with the addition of 'm' meaning minor (major being understood), '+' or 'aug' if augmented and 'o' or 'dim' if diminished. The 3rd and 5th of the triad can be easily deduced so that it is only necessary to identify additional notes with small numbers. Thus in Cmaj7 the major 7th has been added to the triad C, E and G, while in C7 it is the minor 7th that has been added to the triad C, E and G. The performer is free to indulge in melodic and harmonic extemporisation and for this reason jazz notation is not prescriptive - rather it is descriptive of general ideas that might arise from the shape of a melody or from a chord progression. We will return again to these points in lesson 17.
|
|
|
Broken & Spread Chords
::

|
Key words:
broken chord
spread chord
arpeggio |
| 1 |
Broken & Spread Chords
Chords do not have to be played as solid 'blocks' of sound. The performer can spread the chords out into a succession of notes each of which forms the original chord but which are now turned into a 'harmonic' melody. This was a device used often in the seventheenth and eighteenth centuries. The excerpt below produces animation from a sequence of broken chords over a repeated D root in the bass. The bass D is placed high in the chord so that the chords are actually being heard successively in the tenor line in root position, as a first inversion, then a second inversion and finally in root position again an octave higher. This excerpt is from a work for recorders in The Dolmetsch Library. | | | | | Vivaldi, arranged J.S. Bach - Excerpt | | | |
| | | |
|
|
 :: next lesson :: next lesson
| |
 :: next lesson
:: next lesson